Problem C. 874. (November 2006)

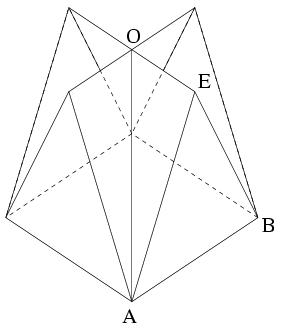
C. 874. The roof of a newsstand with a square base 3 m on a side consists of two regular triangular prisms that intersect each other. One lateral face of each prism coincides with the ceiling of the newsstand. (The prisms are rotated through 90^o relative to each other.) Calculate the surface area of the roof.

(5 pont)

Deadline expired on December 15, 2006.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A tetőfelület nyolc egybevágó, derékszögű háromszögből tevődik össze. Számítsuk ki egy ilyennek a területét:

$t=t_{{\rm AOE}\triang}=0,5\cdot AE\cdot EO=0,5\cdot3\cdot1,5=0,5\cdot4,5~{\rm m}^2.$

A tetőfelület nagysága tehát 8^.0,5^.4,5 m²=18 m².

Ha a felületbe beleszámítjuk a négy egybevágó, 3 m oldalú szabályos háromszög területét is, akkor nagysága $18+4\cdot0,5\cdot3\cdot\frac{\sqrt3}{2}\cdot3~{\rm m}^2=18+9\sqrt3~{\rm m}^2\approx33,59~{\rm m}^2$ .

Statistics:

353 students sent a solution.

5 points: 230 students.

4 points: 76 students.

3 points: 12 students.

2 points: 11 students.

1 point: 6 students.

0 point: 17 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, November 2006

353 students sent a solution.
5 points:	230 students.
4 points:	76 students.
3 points:	12 students.
2 points:	11 students.
1 point:	6 students.
0 point:	17 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?