 Problem C. 878. (December 2006)
Problem C. 878. (December 2006)
C. 878. A cube is inscribed in a regular four-sided pyramid whose height is the double of the length of the sides of its base. What proportion of the volume of the pyramid is occupied by this cube. (The inscribed cube has four vertices on the lateral edges and the other four are lying on the base of the pyramid.)
(5 pont)
Deadline expired on January 15, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Az ábrán a gúla magasságán átmenő,két szemközti lapra merőleges síkmetszete látható.
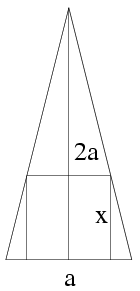
A két hasonló derékszögű háromszögből
ahonnan . Ebből
,
, tehát a kocka térfogata a gúla térfogatának 4/9-e.
Statistics:
341 students sent a solution. 5 points: 291 students. 4 points: 8 students. 3 points: 4 students. 2 points: 5 students. 1 point: 11 students. 0 point: 16 students. Unfair, not evaluated: 6 solutionss.
Problems in Mathematics of KöMaL, December 2006
