Problem C. 886.

Order KöMaL!

ELTE

Competitions Portal

C. 886. The wall of a building is decorated by a square with its circumscribed circle drawn. There is a semicircle drawn outwards on each side of the square as a diameter, so that the circular arcs form four crescent shaped figures. What is the length of the side of the square if the area of such a crescent is 1 m²?

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás. Jelölje a négyzet oldalát x. Ekkor egy Hold alakú mező területe:

$t=\frac{1}{2}\cdot\left(\frac{x}{2}\right)^2\cdot\pi-\left(\frac{1}{4}\cdot \left(\frac{\sqrt2}{2}x\right)^2\pi-\frac{1}{2}\cdot\left(\frac{\sqrt2}{2}x\right)^2\right)=$

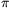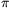=x²( $\pi$ /8- $\pi$ /8+1/4)=x²/4.

Vagyis 1=x²/4, ahonnan x=2 m.

Statistics on problem C. 886.

410 students sent a solution.

5 points: 357 students.

4 points: 8 students.

3 points: 35 students.

2 points: 7 students.

0 point: 2 students.

Unfair, not evaluated: 1 solution.

Problems in Mathematics of KöMaL, February 2007

Our web pages are supported by:

ELTE