Problem C. 895.

Order KöMaL!

ELTE

Competitions Portal

C. 895. The series of diagrams shown is made up of more and more dark regular triangles. The series is continued to the n-th diagram according to the rule that can be observed. How many dark triangles are used altogether?

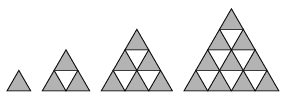
(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás. A sötét háromszögek száma:

$1+(1+2)+(1+2+3)+\cdots+(1+2+\cdots+n)=\frac{2\cdot1}{2}+ \frac{3\cdot2}{2}+\frac{4\cdot3}{2}+\cdots+\frac{(n+1)\cdot n}{2}=$

$=\frac{(1+1)1+(2+1)2+(3+1)3+\cdots+(n+1)n}{2}=\frac{(1^2+2^2+3^2+\cdots+n^2)+1\cdot(1+2+3+\cdots+n)}{2}=$

$=\frac{1}{2}\cdot\left(\frac{n(n+1)(2n+1)}{6}+\frac{(n+1)n}{2}\right)=\frac{n(n+1)(n+2)}{6}.$

Statistics on problem C. 895.

211 students sent a solution.

5 points: 118 students.

4 points: 8 students.

3 points: 8 students.

2 points: 16 students.

1 point: 26 students.

0 point: 10 students.

Unfair, not evaluated: 25 solutions.

Problems in Mathematics of KöMaL, April 2007

Our web pages are supported by:

ELTE