Problem C. 907. (September 2007)

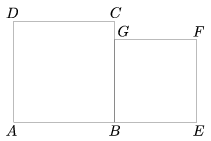
C. 907. The square ABCD of side a and the square BEFG of side b are drawn next to each other as shown in the figure. Express in terms of a and b the area of the quadrilateral formed by the midpoints of the line segments AB, BE, FC and DG.

(5 pont)

Deadline expired on October 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: F₁F₄ az ABGD trapéz középvonala, így párhuzamos AD-vel, és hossza $\frac{AD+BG}{2}=\frac{a+b}{2}$ .

F₂F₃ az EFCB trapéz középvonala, így párhuzamos BC-vel, hossza pedig $\frac{BC+EF}{2}=\frac{a+b}{2}$ .

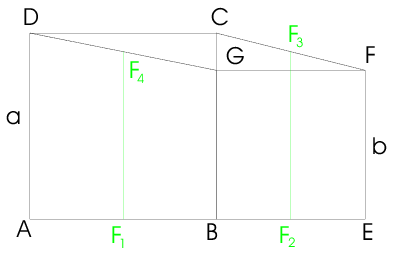
Mivel AD||BC, ezért F₁F₂F₃F₄ két szemben fekvő oldala, F₁F₄ és F₂F₃ párhuzamos és egyenlő, tehát ez a négyszög paralelogramma. Mivel oldalai merőlegesek egymásra ( $F_1F_4||AD\perp AE$ ), ezért téglalap.

F₁F₂=F₁B+BF₂=a/2+b/2, tehát F₁F₂F₃F₄ négyzet. Így területe:

$T=\left(\frac{a+b}{2}\right)^2.$

Statistics:

617 students sent a solution.

5 points: 168 students.

4 points: 84 students.

3 points: 71 students.

2 points: 84 students.

1 point: 69 students.

0 point: 131 students.

Unfair, not evaluated: 10 solutionss.

Problems in Mathematics of KöMaL, September 2007

617 students sent a solution.
5 points:	168 students.
4 points:	84 students.
3 points:	71 students.
2 points:	84 students.
1 point:	69 students.
0 point:	131 students.
Unfair, not evaluated:	10 solutionss.

Already signed up?
New to KöMaL?