Problem C. 918. (November 2007)

C. 918. Connect the midpoints of the sides of a rectangle to the opposite faces. The eight lines obtained in this way form an octagon. What fraction of the whole area of the rectangle is the area of the octagon?

(5 pont)

Deadline expired on December 17, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás: A behúzott nyolc szakasz négy egybevágó részre osztja a téglalapot. Elég az egyik ilyen részt megvizsgálni.

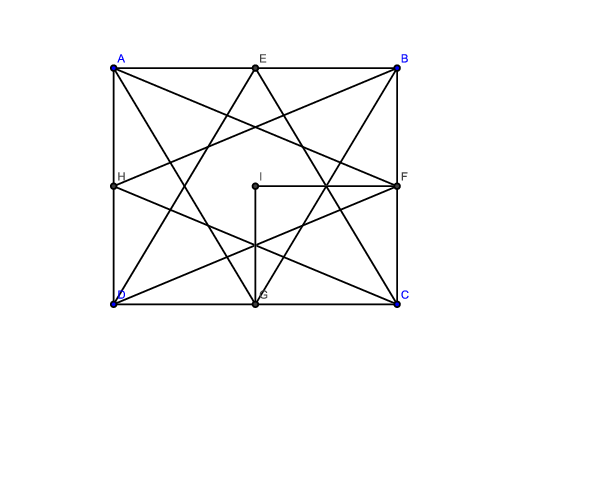
Nyilván BG felezi az IF, HC pedig az IG szakaszt.

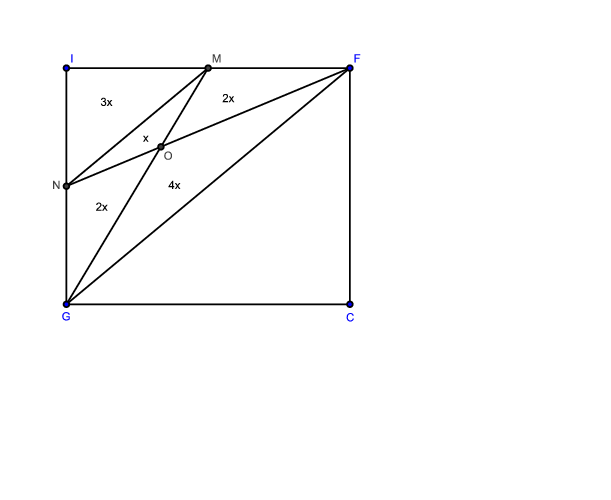
Az IFG háromszög súlyvonalai harmadolják egymást, és felezik a háromszög területét. Legyen az $OMN_{\triangle}$ területe x. Mivel 2NO=OF, ezért 2t_NMO=t_FMO=2x. Mivel MN az $INF_{\triangle}$ súlyvonala, ezért t_IMN=t_OMN+t_OMF=3x.

Innen t_NGF=t_INF=6x.

A keresett arány:

$\frac{3x+x}{2\cdot(3x+x+2x+2x+4x)}=\frac{4x}{24x}=\frac16$ .

A keletkezett nyolcszög területe hatodrésze a téglalap területének.

Statistics:

245 students sent a solution.

5 points: 168 students.

4 points: 15 students.

3 points: 14 students.

2 points: 5 students.

1 point: 14 students.

0 point: 24 students.

Unfair, not evaluated: 5 solutionss.

Problems in Mathematics of KöMaL, November 2007

245 students sent a solution.
5 points:	168 students.
4 points:	15 students.
3 points:	14 students.
2 points:	5 students.
1 point:	14 students.
0 point:	24 students.
Unfair, not evaluated:	5 solutionss.

Already signed up?
New to KöMaL?