 Problem C. 919. (November 2007)
Problem C. 919. (November 2007)
C. 919. A right-angled triangle is cut into a triangle and a quadrilateral by the perpendicular bisector of its hypotenuse. The ratio of the diagonals of the quadrilateral is . Find the acute angles of the right-angled triangle.
(5 pont)
Deadline expired on December 17, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás:
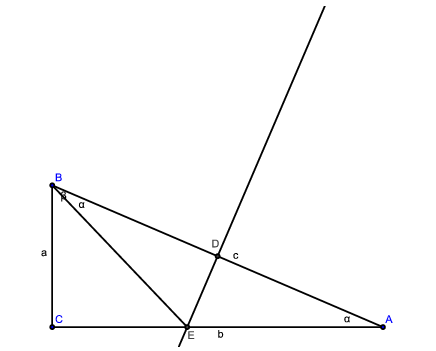
Mivel E rajta van az AB szakasz felező merőlegesén, ezért EBA =BAC
=BAC =
= .
.
, ezért
. A Thalesz-tétel miatt BD=DC, így az átlók aránya
. Tudjuk, hogy
, ezért az átlók aránya:
Mivel
ezért
 =75o,
=75o,
 =15o.
=15o.
Statistics:
274 students sent a solution. 5 points: 232 students. 4 points: 19 students. 3 points: 4 students. 2 points: 4 students. 1 point: 4 students. 0 point: 10 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, November 2007
