C. 937. Three sides of a quadrilateral are , b=9 and . Sides a and b enclose an angle of 30^o, and sides b and c enclose an angle of 90^o. What angle do the diagonals enclose?

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás: Állítsunk D-ben merőlegest AD-re, és ennek az AB oldallal vett metszéspontja legyen E. Mivel az ADE háromszögben DAE=30^o és ADE=90^o, ezért a háromszög harmadik szöge, AED=60^o, és AD ismeretében DE és AE is meghatározható: , illetve DE=AE/2=4.

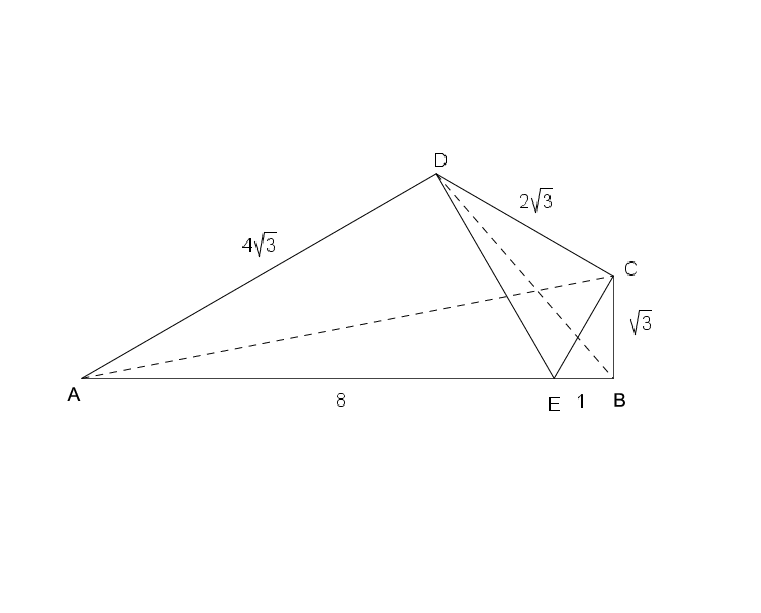
Ezután kössük össze E-t a C ponttal. Az EBC háromszög derékszögű, befogói és 1 hosszúak, így átfogója, EC=2, és ez a háromszög is egy szabályos háromszög fele, CEB=60^o és ECB=30^o.

A DEC háromszög oldalai: EC=2, ED=4 és , tehát ez is egy szabályos háromszög fele, DEC=60^o, DCE=90^o és EDC=30^o.

Tekintsük ezután az ADC és a DCB háromszöget. A két háromszög hasonló, hiszen és ADC=DCB=90^o+30^o=120^o, tehát két oldaluk aránya és az általuk közrezárt szög megegyezik. Ez azt jelenti, hogy van olyan középpontos hasonlósági transzformáció, amely az ADC háromszöget a DCB háromszögbe viszi. Mivel az AD és a DC egyenesek által bezárt szög 180^o-120^o=60^o, ezért az AC és a DB egyenesek által bezárt szög is 60^o.

Statistics on problem C. 937. 224 students sent a solution. 5 points: 138 students. 4 points: 60 students. 3 points: 10 students. 2 points: 8 students. 1 point: 2 students. 0 point: 3 students. Unfair, not evaluated: 3 solutions.