Problem C. 939. (March 2008)

C. 939. A rectangle of sides 15 cm and 20 cm is rotated about a diagonal. What is the volume of the resulting solid of revolution?

(5 pont)

Deadline expired on April 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A téglalap átlója a Pitagorasz-tétel felhasználásával $\sqrt{15^2+20^2}=25$ cm hosszú. Az átlónak a téglalap szimmetria-középpontjától a csúcsig terjedő szakasza ennek fele, vagyis 12,5 cm.

Az átló a téglalapot két egybevágó derékszögű háromszögre bontja. Ezek magassága a területképletek felhasználásával számolható: $t=\frac{15\cdot20}{2}=\frac{25\cdot m}{2}$ , és így m=12. A magasság által a téglalap feléből levágott kisebb derékszögű háromszög hasonló a 15, 20, 25 oldalú háromszöghöz, hiszen szögeik megegyeznek. A hasonlóságból következik, hogy megfelelő oldalaik aránya egyenlő. A magasság által az átfogóból levágott rövidebb szakaszt jelölje y. Ekkor: $\frac {12}{y}=\frac{20}{15}$ , ahonnan y=9.

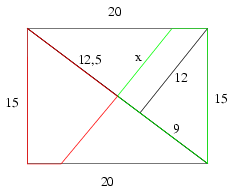
Az átló felének a középpontig terjedő maradék része 12,5-9=3,5 cm hosszú.

A forgatás végeredménye ugyanaz, mintha a zölddel és a pirossal jelölt részeket forgatnánk meg az átló körül. A térfogat kiszámításához ki kell még számítanunk x-et: $\frac{x}{12}=\frac{12,5}{25-9}$ , és így x=9,375.

Így a térfogat:

$V=2\cdot\left[\frac{12^2\pi\cdot9}{3}+\left(\frac{12^2\pi\cdot(25-9)}{3}-\frac{9,375^2\pi\cdot12,5}{3}\right)\right]\approx 5238,85~cm^2.$

Statistics:

205 students sent a solution.

5 points: 121 students.

4 points: 40 students.

3 points: 21 students.

2 points: 11 students.

1 point: 2 students.

Unfair, not evaluated: 10 solutionss.

Problems in Mathematics of KöMaL, March 2008

205 students sent a solution.
5 points:	121 students.
4 points:	40 students.
3 points:	21 students.
2 points:	11 students.
1 point:	2 students.
Unfair, not evaluated:	10 solutionss.

Already signed up?
New to KöMaL?