Problem C. 947.

Order KöMaL!

ELTE

Competitions Portal

C. 947. A rabbit is sitting at a point A, at a distance of 160 m from a straight railway track. The perpendicular projection of A onto the track is T. A train is approaching T at a speed of 30 m/s. The distance of the front of the train from point T is 300 m initially. The rabbit can run at 15 m/s. Can he cross the track in any direction before the train comes?

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás:

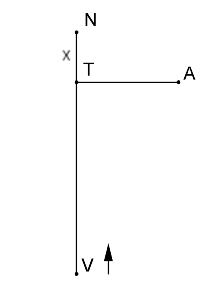
Célozzon meg a nyuszi egy olyan N pontot a síneken, melyre teljesül, hogy T elválasztja N-et és V-t (V-vel jelöljük a vonat elejét). Legyen x=NT. A derékszögű NTA háromszögre felírva a Pitagorasz-tételt: TA²+x²=NA², vagyis $NA=\sqrt{160^2+x^2}$ .

A vonat 300+x méter utat tesz meg 30 m/s sebességgel, $t_v=\frac{300+x}{30}$ másodperc alatt.

A nyuszi NA utat tesz meg 15 m/s sebességgel, $\frac{\sqrt{160^2+x^2}}{15}$ másodperc alatt.

Ahhoz, hogy a nyuszi a vonatnál hamarabb érje el az N pontot, annak kell teljesülnie kell, hogy:

$\frac{300+x}{30}>\frac{\sqrt{160^2+x^2}}{15}.$

30-cal való beszorzás után négyzetre emelve:

90000+x²+600x>102400+4x²,

0>3x²-600x+12400.

$x_{1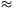,2}=100\pm\frac{\sqrt{211200}}{6},$

x₁ $\approx$ 100+76,59=176,59; x₂ 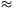$\approx$ 100-76,59=23,41.

Az egyenlőtlenség 23,41<x<176,59 esetén teljesül.

Tehát, ha a nyuszi pl. a T-től 30 méterre levő pontot célozza meg, akkor még a vonat előtt átér a síneken.

Statistics on problem C. 947.

137 students sent a solution.

5 points: 93 students.

4 points: 7 students.

3 points: 19 students.

2 points: 7 students.

1 point: 2 students.

0 point: 9 students.

Problems in Mathematics of KöMaL, May 2008

Our web pages are supported by:

ELTE