 Problem C. 949. (May 2008)
Problem C. 949. (May 2008)
C. 949. The midpoint of the base AB of an isosceles triangle ABC is F, and its orthocentre is M. Given that the centroid of the triangle lies on the inscribed circle and , what may be the lengths of the sides of the triangle?
Suggested by D. Fülöp, Marcali
(5 pont)
Deadline expired on June 16, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Jelölje a beírható kör sugarát r, középpontját O, az O-ból a BC oldalra állított merőleges talppontját H, a háromszög szárát a, végül legyen AF=FB=x az ábra szerint.
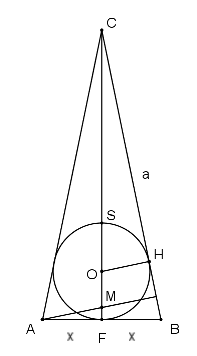
Tudjuk, hogy FS=FC/3 (mert a súlypont harmadolja a súlyvonalat) és FS=2r, emiatt FC=6r, és így OC=6r-r=5r.
, hiszen mindkettő derékszögű háromszög, és a C csúcsnál fekvő szögük is megegyezik. Emiatt
, vagyis
, amiből a=5x.
A CF szakasz hosszát a BCF háromszögben Pitagorasz tétellel kiszámolva: .
Az , mert mindkettő derékszögű, és FAM
 és FCB
és FCB merőleges szárú hegyesszögek, és így egyenlőek. Tehát
merőleges szárú hegyesszögek, és így egyenlőek. Tehát , vagyis
, amiből x=12.
Így a háromszög oldalai: AB=2x=24 és BC=AC=5x=60.
Statistics:
90 students sent a solution. 5 points: 71 students. 4 points: 5 students. 3 points: 6 students. 2 points: 3 students. 1 point: 2 students. 0 point: 3 students.
Problems in Mathematics of KöMaL, May 2008
