Problem C. 953. (September 2008)

C. 953. Given that a right-angled trapezium has an inscribed circle, show that the length of the right-angled leg is the harmonic mean of the lengths of the bases.

(5 pont)

Deadline expired on October 15, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. A kör középpontját jelölje O, az O-ból a trapéz nem derékszögű szárára állított merőleges talppontját T, az alapokra emelt merőlegesek talppontját pedig R, illetve S.

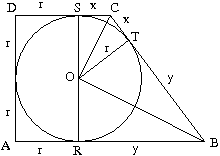
DC a kör érintője, így merőleges SO-ra. Ugyanígy AB merőleges RO-ra. Mivel $DC\parallel AB$ , ezért az O-ból rájuk állított merőlegesek egy egyenesbe esnek: S, O és R egy egyenesen vannak. Az ARSD négyszög téglalap, hiszen szomszédos oldalai merőlegesek egymásra. Ezért AD=RS=2r. Mivel egy pontból a körhöz húzott érintési szakaszok hossza egyenlő, ezért az ábrán látható szakaszok keletkeznek, hosszukat jelölje r (ami egyenlő a beírt kör sugarával), illetve x és y.

COB $\angle$ =180^o-(DCB $\angle$ /2+ABC $\angle$ /2)=180^o-90^o=90^o. A COB háromszögre alkalmazva a magasságtételt kapjuk, hogy r²=xy.

Az alapok hosszának harmonikus közepét felírva, majd átalakítva:

$\frac{2}{\frac{1}{r+x}+\frac{1}{r+y}}=$

$=\frac{2(r+x)(r+y)}{r+y+r+x}=\frac{2(r^2+r(x+y)+xy)}{2r+(x+y)}=$

$=\frac{2(r^2+r(x+y)+r^2)}{2r+(x+y)}=\frac{4r^2+2r(x+y)}{2r+(x+y)}=2r,$

ami épp a derékszögű szár hossza.

Statistics:

382 students sent a solution.

5 points: 236 students.

4 points: 64 students.

3 points: 9 students.

2 points: 13 students.

1 point: 12 students.

0 point: 41 students.

Unfair, not evaluated: 7 solutionss.

Problems in Mathematics of KöMaL, September 2008

382 students sent a solution.
5 points:	236 students.
4 points:	64 students.
3 points:	9 students.
2 points:	13 students.
1 point:	12 students.
0 point:	41 students.
Unfair, not evaluated:	7 solutionss.

Already signed up?
New to KöMaL?