Problem C. 957.

Order KöMaL!

ELTE

Competitions Portal

C. 957. The sides of a rectangle are a and b. Two congruent circles are placed in a rectangle so that they have no interior point in common. What is the ratio of the sides of the rectangle if the diameter of the largest possible circles is $d=\frac25a+\frac16b$ ?

(5 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás. I. eset: a két kör csak "ferdén" fér bele az ABCD téglalapba. Jelölje a téglalapba rajzolt két kör középpontját E és G. Húzzuunk párhuzamost AB-vel E-n keresztül és BC-vel G-n keresztül, ezek metszéspontja legyen F, a téglalap oldalaival vett metszéspontok pedig az ábra szerint H, I, J és K.

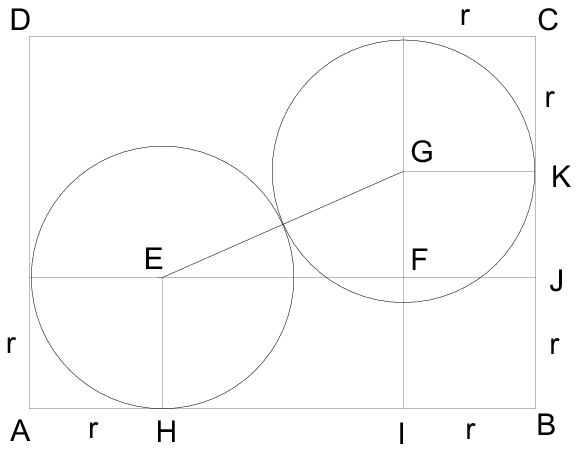
Mivel AH=IB=r, így HI=AB-2r. A párhuzamosság miatt HIFE téglalap, így EF=HI. Tehát EF=AB-2r.

Hasonlóan belátható, hogy FG=BC-2r.

Legyen AB=a, BC=b és tekintsük az EFG derékszögű háromszöget. (Mivel $FG\parallel BC$ és $EF\parallel AB$ és $AB\perp BC$ , ezért $AF\perp FG$ .) Írjuk fel rá a Pitagorasz-tételt:

(2r)²=(b-2r)²+(a-2r)².

Használjuk fel, hogy $2r=\frac25a+\frac16b$ . Ezzel az egyenlet így alakul:

$\left(\frac25a+\frac16b\right)^2=\left(\frac56b-\frac25a\right)^2+\left(\frac35a-\frac16b\right)^2,$

amit tovább alakítva kapjuk, hogy:

$0=\frac{9}{25}a^2+\frac{25}{36}b^2-ab.$

Az egyenlet mindkét oldalát osztva a²-tel és szorozva 25^.36-tal kapjuk, hogy:

$0=625\cdot\left(\frac ba\right)^2-900\cdot\frac ba+324,$

amiből $\frac ba=\frac{18}{25}$ .

Ezekkel az adatokkal mind a-2r, mind b-2r pozitív lesz, tehát lehetséges elrendezést kapunk.

II. eset: b>a, és mindkét kör átmérője a-val egyenlő. Ekkor:

$a=\frac25a+\frac16b,$

amiből

$\frac ba=\frac{18}{5}.$

III. eset: b<a, és mindkét kör átmérője b-vel egyenlő. Ekkor:

$b=\frac25a+\frac16b,$

amiből

$\frac ab=\frac{25}{12}.$

Statistics on problem C. 957.

328 students sent a solution.

5 points: Al-Taani Szábit, Bálint Csaba, Bárány Ambrus, Benyó Krisztián, Berghammer Tamás, Blóz Gizella Evelin, Böröcz 369 Bence, Csere Kálmán, Demeter Balázs, Egyed Zsombor, Farkas Zsuzsanna, Gubicza Krisztina, Handler Balázs, Karkus Zsuzsa, Kis-Pál Tamás, Lőrincz Dóra, Nagy-György Péter, Németh Nóra, Orosz Ákos, Pálovics Péter, Poócza Eszter, Pósfai Balázs, Regele János, Sáfár Kinga, Samu Viktor, Somogyi Ákos, Szepesvári Eszter, Szepesvári Réka, Tolnai Dániel, Várnai Péter, Végh János, Zsupanek Alexandra.

4 points: Árvay Balázs, Botond Ákos, Csanády Bálint Zsombor, Finok Orsi, Gaizer Bence, Gergely Lívia, Lantos Tamás, Máté Márta, Mayer Martin János, Medvey Fanni, Mihálka Éva Zsuzsanna, Morapitiye Sunil, Németh 144 Bálint, Orbán Réka, Schwarcz Gergő, Sváb Gergely, Vajda Ildikó.

3 points: 7 students.

2 points: 77 students.

1 point: 120 students.

0 point: 67 students.

Unfair, not evaluated: 8 solutions.

Problems in Mathematics of KöMaL, October 2008

Our web pages are supported by:

ELTE