 Problem C. 968. (December 2008)
Problem C. 968. (December 2008)
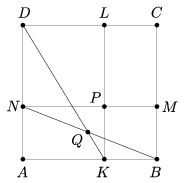
C. 968. As shown, the square ABCD is divided, with lines parallel to its sides, into the squares NPLD and KBMP, and two congruent rectangles. Let P denote the intersection of KL and MN, and let Q be the intersection of BN and DK. Show that the points C, P and Q are collinear.
(5 pont)
Deadline expired on January 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Három pár egybevágó téglalappárt látunk az ábrán, amelyek egymás 90o-os elforgatottjai: MCDN és LDAK, KBCL és BMNA, valamint PMCL és KPNA. Ezért a megfelelő átlók merőlegesek egymásra. Vagyis ,
. Ezért a KCN háromszögben Q magasságpont. Mivel
, ezért a PC egyenes a harmadik magasság, vagyis átmegy a Q ponton. Azaz a C, P és Q pontok valóban egy egyenesre illeszkednek.
Statistics:
129 students sent a solution. 5 points: 89 students. 4 points: 1 student. 2 points: 4 students. 1 point: 2 students. 0 point: 28 students. Unfair, not evaluated: 5 solutionss.
Problems in Mathematics of KöMaL, December 2008
