Problem C. 976. (February 2009)

C. 976. The sum of three positive numbers is multiplied by the sum of their reciprocals. Find the smallest possible interval where the product may lie.

(5 pont)

Deadline expired on March 16, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Néhány számhármas kipróbálása utáni sejtésünk:

$(a+b+c)\left(\frac 1a+\frac 1b+\frac 1c\right)\geq9.$

Beszorzás után kapjuk, hogy:

$1+\frac ab+\frac ac+\frac ba+1+\frac bc+\frac ca+\frac cb+1\geq9.$

A tagokat átcsoportosítva:

$3+\left(\frac ab+\frac ba\right)+\left(\frac ac+\frac ca\right)+\left(\frac bc+\frac cb\right)\geq9.$

Egy pozitív szám és reciprokának összege legalább 2, tehát az egyenlőtlenség igaz.

A szorzat pedig bármilyen n egész számnál nagyobb lehet, hiszen ehhez elég, ha például a=nb teljesül.

Vagyis a legszűkebb intervallum, ahova a szorzat eshet: [9;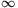 $\infty$ [.

Statistics:

192 students sent a solution.

5 points: 74 students.

4 points: 46 students.

3 points: 45 students.

2 points: 13 students.

1 point: 5 students.

0 point: 5 students.

Unfair, not evaluated: 4 solutionss.

Problems in Mathematics of KöMaL, February 2009

192 students sent a solution.
5 points:	74 students.
4 points:	46 students.
3 points:	45 students.
2 points:	13 students.
1 point:	5 students.
0 point:	5 students.
Unfair, not evaluated:	4 solutionss.

Already signed up?
New to KöMaL?