Problem C. 979. (February 2009)

C. 979. We have a red bouncy ball with thirty round white spots on it. (The spots form spherical caps.) The perimeter of the great circle of the ball is 54 cm, and the perimeter of the spots is 11 cm. What percentage of the surface area of the ball is covered by the spots?

(5 pont)

Deadline expired on March 16, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Jelölje a labdának megfelelő gömb sugarát r, a pöttynek megfelelő gömbsüveg alapkörének sugarát $\varrho$ , magasságát pedig m.

r és $\varrho$ közvetlenül számolható:

$r=\frac{54}{2\pi}\approx8,59;\qquad\qquad\varrho=\frac{11}{2\pi}\approx1,75.$

Messük el a gömböt egy, a középpontján és egy gömbsüveg alapkörének középpontján átmenő síkkal.

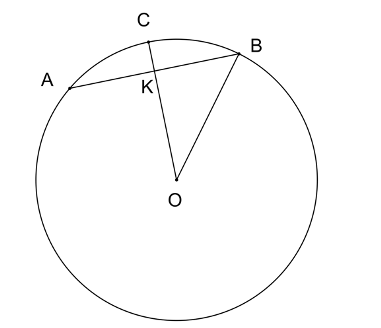
Használjuk az ábra jelöléseit. Ekkor OB=OC=r, KB= $\varrho$ és KC=m. Ebből OK=r-m. Írjuk fel a Pitagorasz-tételt az OKB háromszögre:

r²= $\varrho$ ²+(r-m)²,

amiből

$r-m=\sqrt{r^2-\varrho^2}\approx8,41,$

és így m=r-8,41=0,18.

Egy pötty felszíne:

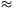A_p=2 $\pi$ rm $\approx$ 9,72,

a labda felszíne:

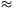A_l=4 $\pi$ r² $\approx$ 927,25.

A keresett arány: $\frac{30\cdot9,72}{927,25}\approx31,45\%$ .

Statistics:

254 students sent a solution.

5 points: 152 students.

4 points: 53 students.

3 points: 11 students.

2 points: 23 students.

1 point: 7 students.

0 point: 3 students.

Unfair, not evaluated: 5 solutionss.

Problems in Mathematics of KöMaL, February 2009

254 students sent a solution.
5 points:	152 students.
4 points:	53 students.
3 points:	11 students.
2 points:	23 students.
1 point:	7 students.
0 point:	3 students.
Unfair, not evaluated:	5 solutionss.

Already signed up?
New to KöMaL?