Problem C. 983. (March 2009)
C. 983. Given the line BD and the feet of the perpendiculars dropped from point A onto line CD, from point B onto line DA, from point C onto line AB and from point D onto line BC, construct the quadrilateral ABCD. (It is not required to discuss the number of possible solutions.)
(5 pont)
Deadline expired on April 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Induljunk ki az ABCD négyszögből, és vizsgáljuk meg, hogy mi van megadva. Jelölje a megfelelő talppontokat rendre A', B', C' és D'.
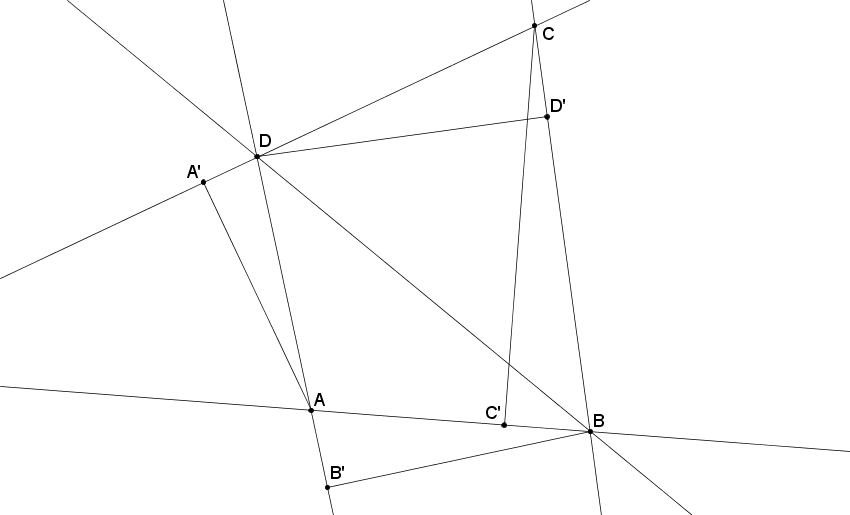
Mivel BB'D
=BD'D=90o, azért a Tálesz-tétel megfordítása miatt B' és D' illeszkedik a BD, mint átmérő fölé írt körre. A kör középpontját a B'D' felező merőlegesének és a BD egyenesnek a metszéspontjaként megkapjuk. Jelölje O ezt a középpontot.
Mivel OB=OD=OD'=OB', ezért az O középpontú, OB' sugarú kör kimetszi a BD egyenesből B-t és D-t.
Mivel C illeszkedik az A'D és a D'B egyenesre is, ezért e két egyenes metszéspontjaként megkapjuk.
Az A pont pedig a C'B és a B'D egyenesekre illeszkedik, tehát e két egyenes metszéspontjaként kapjuk meg.
Statistics:
116 students sent a solution. 5 points: 89 students. 4 points: 2 students. 2 points: 1 student. 1 point: 10 students. 0 point: 7 students. Unfair, not evaluated: 7 solutionss.
Problems in Mathematics of KöMaL, March 2009