Problem C. 993. (May 2009)

C. 993. The midpoint of the base AB of an isosceles triangle ABC is F. Let D denote the orthogonal projection of point F onto side BC. Let E be the midpoint of the line segment DF. Prove that CE is perpendicular to AD.

(5 pont)

Deadline expired on June 15, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Legyen H az A csúcs BC oldalra eső merőleges vetülete.

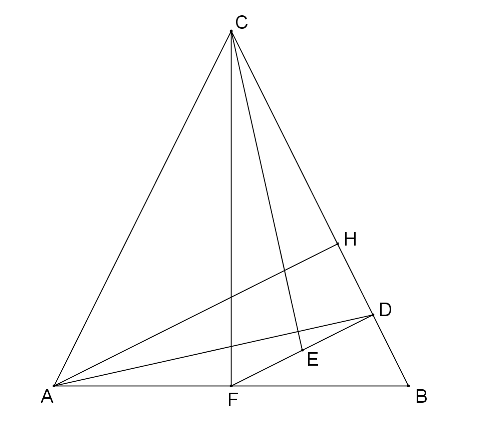
$ABH\triangle\approx CFD\triangle$ , mert szögeik egyenlők. (HAB $\angle$ =DCF $\angle$ =90^o- $\beta$ és BHA $\angle$ =FDC $\angle$ =90^o.)

Mivel AD és CE két hasonló háromszög megfelelő súlyvonalai, ezért $ADH\triangle\approx CED\triangle$ . Ebből következik, hogy HAD $\angle$ =DCE $\angle$ . Tudjuk még, hogy $AH\perp DC$ , és így HAD és DCE szögek merőleges szárú szögek, tehát a másik két száruk is merőleges egymásra.

Statistics:

78 students sent a solution.

5 points: 69 students.

4 points: 4 students.

3 points: 1 student.

2 points: 1 student.

1 point: 1 student.

0 point: 1 student.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, May 2009

78 students sent a solution.
5 points:	69 students.
4 points:	4 students.
3 points:	1 student.
2 points:	1 student.
1 point:	1 student.
0 point:	1 student.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?