 Problem G. 603. (May 2017)
Problem G. 603. (May 2017)
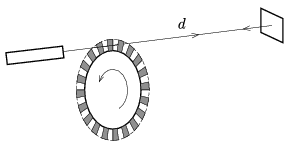
G. 603. A finely wrought cogwheel is rotated, its teeth cease a thin laser beam travelling through them. The beam is reflected in a mirror at a distance of \(\displaystyle d=1000\) m from the wheel such that it arrives at its starting point through the same gap between the teeth. The speed of the wheel is increasing uniformly and 1 minute after its start it reaches the value of 600 rotations per second. How long does it take after starting the wheel, until the reflected beam on the side of the light source disappears? There are 300 teeth on the wheel, and the size of a tooth is the same as the size of a gap.
(3 pont)
Deadline expired on June 12, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A fény sebessége \(\displaystyle 300\,000\) km/s, tehát a tükörig és vissza összesen
\(\displaystyle \Delta t= \frac{2\cdot 1000~\rm m}{300\,000~\rm km/s}=6{,}67\cdot10^{-6}~\rm s\)
idő alatt jut el a fény. Ha ezalatt a korong egy fognyit (a teljes kör 1/600-ad részét) fordul el, a visszaérkező fénysugár már nem juthat át a fogak között. Ez akkor következik be, amikor a korong körülfordulási ideje
\(\displaystyle T=600\cdot \Delta t=0{,}004~\rm s,\)
vagyis a fordulatszáma: \(\displaystyle f=1/T=250~1/\rm s\). Ezt a forgási sebességet az indítástól számított 25 másodperc múlva éri el az egyre gyorsabban forgó korong.
Statistics:
16 students sent a solution. 3 points: Békési Péter, Fekete András Albert, Fialovszky Márk, Geretovszky Anna, Kozák 023 Áron, Merkl Levente, Pácsonyi Péter, Rusvai Miklós, Šárai Krisztina, Szakáll Lili, Tanner Norman, Urszuly Csenge. 2 points: Bonifert Balázs, Földesi András, Horváth 999 Anikó. 1 point: 1 student.
Problems in Physics of KöMaL, May 2017
