 Problem G. 604. (May 2017)
Problem G. 604. (May 2017)
G. 604. There are two small objects on an \(\displaystyle L=3\) m-long wooden board, supported at its middle by a wedge. The masses of the objects are \(\displaystyle m_1=0.2\) kg and \(\displaystyle m_2=0.3\) kg. Between the objects there is a compressed small spring of negligible mass. The spring is compressed to a length of \(\displaystyle \ell=0.3\) m, and tied with a thread. The wedge is exactly below the centre of mass of the system.
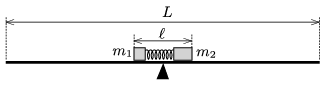
The thread is burnt, and the spring launches the object with mass \(\displaystyle m_1\) at a speed of \(\displaystyle v_1=2\) m/s. To which direction and when will the board be tilted? (Friction is negligible.)
(3 pont)
Deadline expired on June 12, 2017.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A deszka tömegközéppontja is és a két kicsi test tömegközéppontja is az ék fölött van. Kezdetben az \(\displaystyle m_1\) tömegű test a deszka bal szélétől \(\displaystyle s_1=1{,}32\) m távol van, az \(\displaystyle m_2\) tömegű test a deszka jobb szélétől \(\displaystyle s_2=1{,}38\) m távol található.
A fonál elégetése után a rugó szétlöki a két testet, sebességük (a lendületmegmaradás törvénye szerint) \(\displaystyle v_1=2~\)m/s és \(\displaystyle v_2=1{,}33~\)m/s. Az erős rugó gyakorlatilag hosszának elhanyagolható megnövekedése után és igen rövid idő alatt löki szét a testeket. A szétlökött testek egyenletes mozgással közelednek a deszka végeihez, miközben a rendszer tömegközéppontja az ék fölött marad. A deszka csak akkor kezd el billenni, mikor valamelyik test eléri a deszka végét. Ez az \(\displaystyle m_1\) tömegű testtel történik meg előbb, a szétlökődéstől számított
\(\displaystyle t_1=\frac{s_1}{v_1}=0{,}66~\rm s\)
idő múlva. (A másik test csak 1,03 s alatt érné el a deszka szélét, ha a deszka nem billenne el már hamarabb.)
A deszka tehát kb. 0,7 másodperc múlva kezd el jobbra billenni.
Statistics:
20 students sent a solution. 3 points: Bálint Boglárka Eszter, Békési Péter, Fekete András Albert, Fialovszky Márk, Geretovszky Anna, Horváth 999 Anikó, Kozák 023 Áron, Kozmér Barbara, Merkl Levente, Pácsonyi Péter, Rusvai Miklós, Šárai Krisztina, Szakáll Lili, Urbán István, Vida Tamás. 2 points: Bonifert Balázs, Tanner Norman. 1 point: 2 students. 0 point: 1 student.
Problems in Physics of KöMaL, May 2017
