 Problem I/S. 4. (December 2015)
Problem I/S. 4. (December 2015)
I/S. 4. Someone placed \(\displaystyle K\) (\(\displaystyle 0\le K\le 10\;000\)) boxes in a rectangular area of size \(\displaystyle N\times M\) (\(\displaystyle 10\le N, M\le 100\;000\)). Each box has unit height, but their width and length can vary. The sides of the boxes are parallel to the sides of the rectangle. The boxes do not touch each other, and they cannot be observed from above-only from the side-because they have been covered.
Your program is4 should determine the number of boxes that cannot be seen even if we examine the rectangle from all four directions. To spot a box, it is enough to see a part of its face. We can look into the rectangle only perpendicularly to one of its side, and in a straight line.
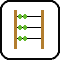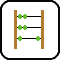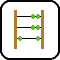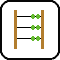
In the example, the striped boxes are visible, and the gray ones are invisible from outside.
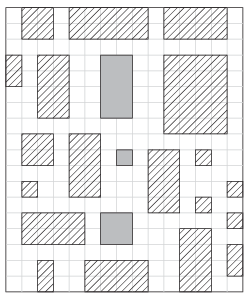
Your program should read the values of \(\displaystyle N\), \(\displaystyle M\) and \(\displaystyle K\) from the first line of the standard input, then-from the following \(\displaystyle K\) lines-the \(\displaystyle X\) and \(\displaystyle Y\) coordinates (positive integers) of the upper left and lower right vertices of the boxes. The first and only line of the standard output should contain the number of invisible boxes. Your program should solve this task within 1 second of running time.

The source code and documentation of your program-containing a brief description of your solution, and the name of the developer environment to compile your code-should be submitted in a compressed file is4.zip.
(10 pont)
Deadline expired on January 11, 2016.
Statistics:
18 students sent a solution. 10 points: Erdős Márton, Gergely Patrik, Janzer Orsolya Lili, Kovács 246 Benedek, Mernyei Péter, Nagy Ábel, Nagy Nándor, Németh 123 Balázs, Noszály Áron, Olexó Gergely, Zarándy Álmos. 8 points: 3 students. 7 points: 2 students. 5 points: 2 students.
Problems in Information Technology of KöMaL, December 2015
