 Problem I. 103. (April 2005)
Problem I. 103. (April 2005)
I. 103. A square lattice of size mxn (with positive integers m and n) is given and unit square based columns are put onto each square. The front and side views of this bar chart-like solid are represented by the numbers u1, u2, ..., um and v1, v2, ..., vn, where ui and vj denote the heights of the rectangles being shadows of the columns.
Write a program whose input consists of the numbers m, n, further the numbers u1, u2, ..., um and v1, v2, ..., vn (in the same format as in problem I. 100.), then it computes the matrix describing heights of the columns of the (or, a possible) solid of minimal volume. If no such solid exists, your program should mark the inconsistent numbers in the data.
Notice that this is again a converse of problem I. 98., where a matrix describing the heights of individual columns was given and we had to display the front and side views of the solid. Now we have to reconstruct the solid of minimal volume from the front and side views.
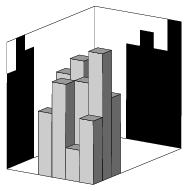
A text file (i103.txt) is to be submitted containing the precise description of the algorithm (5 points), further, the detailed justification of the fact that your algorithm always correctly decides whether the/a solid exists, and, if it does, the algorithm produces a solid with required property (8 points). Your program (i103.pas, ...) should also be submitted (4 points).
(17 pont)
Deadline expired on May 17, 2005.
Statistics:
7 students sent a solution. 17 points: Stippinger Marcell, Ureczky Bálint. 13 points: 2 students. 10 points: 1 student. 9 points: 1 student. 4 points: 1 student.
Problems in Information Technology of KöMaL, April 2005
