 Problem I. 120. (December 2005)
Problem I. 120. (December 2005)
I. 120. We take a loan of S Euro at p per cent compound interest for n months. We pay back the loan in equal monthly installments: the first installment is paid back at the end of the first month, and the installment is at the end of the
month. Before paying back an installment, the bank capitalizes the loan, that is, first our debt is increased according to the rate of interest, only then is the currently paid back sum subtracted from the debt, which is finally rounded up to a nonnegative integer.
Prepare an OpenOffice or Excel sheet summarizing our debt in the course of time. The user enters the initial sum S of the loan, the compound interest rate p and the loan duration n into cells A2, B2 and C2, respectively. Cell E2 should contain the monthly installment, while column B should contain the current debt after paying an installment. Change of the debt should also be graphed in cells C4...F15. In its first row and column some remark should be visible explaining the meaning of the graph.
Example:
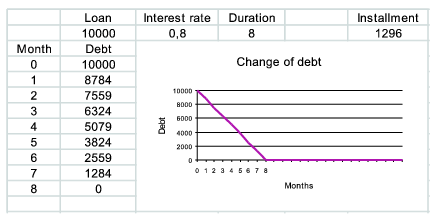
You should submit the sheet (i120.sxc, i120.xls, ...). The value of n can be assumed to lie between 3 and 24. Cases when the interest rate p is 0 should also be handled correctly.
(10 pont)
Deadline expired on January 16, 2006.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. A feladatban a törlesztő részlet pontos kiszámítása okozta a legtöbb nehézséget.
Ha nem lenne kerekítés, a törlesztő összeg p=0 esetén , p
 0 esetén pedig
0 esetén pedig lenne.
A lefelé kerekítések miatt a helyes törlesztő részlet legalább ennyi. A t felső egész része logikus választás, de nem mindig helyes: a lefelé kerekítések miatt bizonyos esetekben a futamidő végén néhány forint adósság marad, ment minden hónapban elvesztünk egy 1 forintnál kisebb összeget. Akik ezt nem vették figyelembe, 8 pontot kaptak.
Ugyanakkor azt sem nehéz meggondolni, hogy ha a törlesztő részletet még 1 forinttal nagyobbnak választjuk, akkor minden hónapban legfeljebb akkora az adósság, mint a kerekítés nélküli esetben, ilyenkor tehát nem maradhat adósságunk.
Összefoglalva, kétféle érték közül kell választanunk. A legtöbb versenyző ezt úgy oldotta meg, hogy egy elrejtett oszlopban kiszámolta az adósság alakulását a kisebbik értékkel, és a táblázat látható részében az alapján választotta meg a törlesztő részletet, hogy a rejtett oszlopban maradt-e adósság a végén.
Fábián András (Szeged, Radnóti M. Kísérleti Gimn. és Ált. Isk, 9. o.) megoldása
Kacz Krisztián (Révkomárom, Selye János Gimn. 12.o.) megoldása
Vincze János (Debrecen, Fazekas M. Gimn. 11. o.) megoldása
Statistics:
20 students sent a solution. 10 points: Czigler András, Kacz Krisztián, Vincze János. 8 points: 5 students. 7 points: 5 students. 6 points: 1 student. 5 points: 2 students. 1 point: 1 student. 0 point: 3 students.
Problems in Information Technology of KöMaL, December 2005
