Problem I. 164. (September 2007)

I. 164. Let us consider the following type of cellular automaton on a 27×27 grid. There are at most two cells living in each square. The uppermost edge of the board is identified with the lowermost one, and similarly, the leftmost with the rightmost. In regular time intervals the whole grid is updated and new cells are formed. Each cell in each step divides into four. The 4 offsprings appear in the 4 neighbouring squares and the parent cell dies. If there are more than 3 newborn cells in a square, they kill each other by threes, until 1 or 2 cells remain.

Write a program to simulate the evolution of the automaton up to N generations. Data is read from the standard input. The first input line is the number of generations N () to simulate. Each of the following 27 lines contains 27 digits (being ``0'', ``1'' or ``2''), encoding the number of living cells in those squares. The output is written to the standard output in the same format.

The simulation should be fast even for large values of N: you can recognize patterns to make the computation faster. We present a only smaller example here.

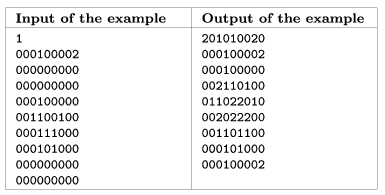
A full board of size 27×27 can be downloaded from the Internet.

The source code of your program (i164.pas, i164.cpp, ...) together with a short documentation (i164.txt, i164.pdf, ...) should be submitted, specifying also which developer environment can be used to compile your program.

27×27 example input

27×27 example output

(10 pont)

Deadline expired on October 15, 2007.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás

Mintamegoldásként Nagy Zoltán (Kaposvár, Munkácsy Mihály Gimnázium és Szakközépiskola, 11. osztály) C nyelven készült munkáját, illetve a hivatalos (C++ nyelven készült) mintamegoldást közöljük.

A szabályosság

A feladat szövegében több helyen utaltunk rá, az N-re vonatkozó korlátokkal és a holnapon szereplő tesztadattal implicite, a feladat szövegezésének végén pedig explicite, hogy a paraméterek ezen értékei mellett a játék valamilyen szabályosságot mutat.

Ahogy azt sokan jól észrevették, ez a szabályosság az volt, hogy a játéktér 27 generációnként periodikusan ismétlődött.

A matematikai igazoláshoz útmutatást nyújt Kós Géza "Kutyák a Marsról" című cikke, mely honlapunkon már régóta olvasható. Ott megmutattuk, hogy az osztódási eljárást végezhetjük minden egyes sejtre külön-külön, és a végén összegezhetjük az eredményeket maradékképzéssel, illetve, hogy a modulo 2 világban egy sejtnek 2^N lépésenként pontosan 4 utódja lesz, amelyek az eredeti sejttől fel, le, jobbra és balra helyezkednek el, mégpedig attól 2^N távolságra.

Hasonlóképp megmutatható, hogy a modulo 3 világban egy ezzel analóg szabály érvényes: 3^N lépésenként pontosan 4 utódja lesz minden sejtnek, az eredeti sejttől fel, le, jobbra és balra, attól 3^N távolságra. Mivel a játéktér 27 egység széles (és magas), ezt azt jelenti, hogy 3³=27 lépést végrehajtva egy sejt 4 utóda épp az őssejtnek megfelelő helyre kerül. Közülük hárman elpusztítják egymást, így összesen 1 marad. Mivel ez minden sejtre igaz, innen már rögtön adódik, hogy a játéktéren 27 lépést végrehajtva visszajutunk a kiindulási állapothoz.

Természetesen jóval egyszerűbb módon, próbálgatás útján is eljuthatunk ehhez a megfigyeléshez. Sőt, akár a programra is rábízhatjuk a feladatot: eltároljuk a kiindulási állapotot, és ha P lépés múlva ugyanaz áll elő, akkor megtaláltuk a periódust, a maradék N-P lépés helyett pedig csak annak P-re adott osztási maradékának megfelelő számút hajtunk végre.

A szabályosságot az utolsó teszteset megoldása során kellett kihasználni, ahol N=1000000000 volt. Ez a teszteset 2 pontot ért.

Típushibák, tanulságok

A problémák, a szabályosság fel nem fedezését nem tekintve, alapvetően három kategóriába sorolhatóak.

Nagyon sok megoldásban maradtak olyan, kisebb-nagyobb hibák, amelyeket a versenyzők egy kicsit több teszteléssel biztosan észrevettek volna, így azonban azt eredményezték, hogy a program a tesztesetek túlnyomó többségében helytelen eredményt produkált. Volt olyan megoldás is, amelyben 1 karakter elírása vezetett hibás működéshez, más programokban ezt egy tömb elindexelése, két ciklus felcserélése, illetve ehhez hasonló trivialitások okozták. A hiba nagyságától függően ezért 2-4 pontot vontunk le. Kérünk titeket, hogy a továbbiakban próbáljatok meg egy kicsivel több időt fordítani a program tesztelésére, élesztésére!

Néhány megoldás nem kezelte helyesen a specifikált tartomány határeseteit, ami jelen esetben az N=0 esetét jelentette. Ekkor természetesen a bemenetként kapott mátrixot kellett egy az egyben visszaadni.

A problémák legnagyobb része azonban specifikáció be nem tartásából származott. Noha ezért leggyakrabban nem, illetve kevés pontot vontunk le, kérjük, erre a továbbiakban sokkal jobban ügyeljetek!

Sok program a standard bemenet és kimenet használata helyett fájlból olvasta és fájlba írta az eredményt. Ezért 1 pont levonás járt.

Ezen kívül majdnem minden programnál volt valamilyen kisebb probléma a be- és/vagy kimenettel. Nagyon sok program extra szóközöket, újsorokat, elválasztó vonalakat, szövegeket írt ki, a futás végén billentyűleütésre várt. Amennyiben a feladat szövegében a be- és kimenetet pontosan definiáljuk, úgy a program a bemenetet mindig a specifikált formában fogja kapni, így azt nem kell ellenőrizni, illetve a kért kimeneten kívül semmi mást nem kell kiírni.

A specifikáció pontos betartására azért van szükség, mert a javítást - legalábbis a program helyes működésének ellenőrzését - igyekszünk automatizálni. Ez viszont csak úgy lehetséges, ha a programokat egységes módon tudjuk lefuttatni a tesztadatokra: azaz ha a program külön felhasználói beavatkozás nélkül képes beolvasni a bemenetet, a kimenetben a specifikált formátumban szerepelnek a kért adatok, illetve ezen túl semmi más nem szerepel. Kérünk titeket, hogy a megoldás során használt debug információk kiírását, illetve a billentyűleütésre várakozásokat is legalább kommentezzétek ki!

Engedy Balázs

cell.cpp

nagy.zip

Statistics:

21 students sent a solution.
10 points:	Adrián Patrik, Juhász Péter, Nagy Zoltán, Véges Márton.
9 points:	Hodosy Gábor.
8 points:	4 students.
7 points:	5 students.
6 points:	1 student.
5 points:	2 students.
4 points:	3 students.
2 points:	1 student.

Problems in Information Technology of KöMaL, September 2007