Problem I. 205. (February 2009)
Problem I. 205. (February 2009)
I. 205. A cellular automaton is a collection of identical cells. Every cell has a state which evolves in each simulation step according to a rule. A rule specifies the state of a cell in the next step based on the current state of the cell and its neighbours. The states of cells are updated simultaneously in each simulation step.
In our model, a one-dimensional cellular automaton is considered, where each cell has two states, 1 or 0. Each generation is displayed in one line. The state of a cell in the next step depends on the state of the cell and its two neighbours. The first and last cells in each generation are always 0.
In the figures, ``környezet'' is neighbourhood, ``vizsgált cella'' is the actual cell, ``állapot'' is state, while ``eredmény'' is the updated state.
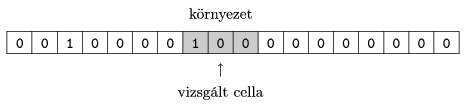
The actual cell and its two neighbours can have 23=8 different states. In the example, Rule 30 is shown: the states in the neighbourhood specify the updated state of the actual cell in the next step.

There are altogether 28=256 rules. Rules are numbered according to the second line of this table: the updated states are interpreted as a binary number, for example 00011110 in binary is 30 in decimal.
The behaviour of a cellular automation is determined by both the initial state and the rule. The long-term behaviour of an automaton can be stable, periodic, random, but complex or self-similar patterns may also emerge.
Your task is to simulate 150 generations of a one-dimensional cellular automaton by using a spreadsheet application. You should use two sheets: sheet ``Rule'' should contain the description of the rule in cells A1:I2 in a similar format to the example above. The second ``Simulation'' sheet should contain consecutive generations in cells A1:ET150 by using a copyable formula. The first and last columns should always contain a 0. The first line contains the initial state. Column widths and heights of lines should be chosen so that cells are visible squares on the screen. Use conditional formatting for the graphics.
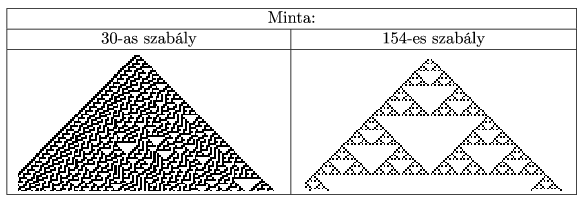
In the example (``Minta''), Rule 30 is ``30-as szabály'' and Rule 154 is ``154-es szabály''.
The sheet (i205.xls, i205.ods, ...) together with a short documentation (i205.txt, i205.pdf, ...) should be submitted, also containing a brief description of your solution and the name and version number of the spreadsheet application. You should include an interesting initial state and rule as well.
(10 pont)
Deadline expired on March 16, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról:
Sok jó megoldás érkezett a feladatokra. A leírásokban sajnos kevés szép és érdekes ábrához tartozó szabályról történt említés.
|
Minta megoldás leírása Balla Attila 11. osztályos tanuló (Budapest, Berzsenyi Dániel Gimnázium) alapján:
Először létrehoztam a szabály munkalapot és elkészítettem az A1:I2 tartományba az állapot-eredmény táblázatot.
Létrehoztam a szimuláció munkalapot az A1:A150 és ET1:ET150 tartományokat feltöltöttem 0-val. A B2:ES150 tartomány celláinak értékeit függvénnyel határozom meg, mégpedig a következő módon: az összefűz függvény segítségével, megkapom azt a háromjegyű számot, ami megadja, hogy az adott cella és szomszédjai milyen értéket vettek fel az előző lépésben. Ezt a háromjegyű számot a VKERES() függvény segítségével megkeresem az állapot-eredmény táblázat állapot sorában, és az alatta lévő eredményt adom a cella értékéül.
Feltételes formázás segítségével a szimuláció munkalap A1:ET150 tartományában a 0 értékű cellákat fehérre, az 1 értékűeket feketére színeztem, valamint a sorok és oszlopok méretét egységesen 10 képpontra állítottam.
Mintamegoldás: i205.xls
Statistics:
16 students sent a solution. 10 points: Balla Attila, Fehér Péter, Janosov Milán, Kővágó Zoltán, Molnár Gábor, Pap 999 Dávid, Póta Kristóf, Sándor Imre, Seres Márk Dániel, Szabó 928 Attila, Tóth Szabolcs, Uray Marcell János. 9 points: Barta 111 János, Englert Péter, Horváth 135 Loránd. 4 points: 1 student.
Problems in Information Technology of KöMaL, February 2009