Problem I. 214. (May 2009)
I. 214. There are N points in a square arranged arbitrarily. One can always draw a polygon around each point such that interior points of this polygon are closer to the actual point that to any other of the N-1 points. These polygons are convex and completely fill the square.
Given a square of size M×M (10
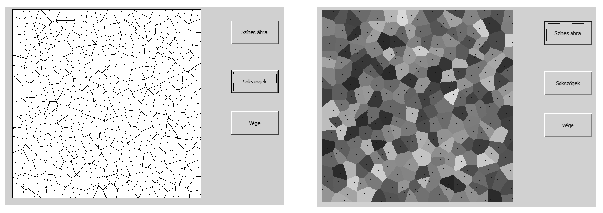
M600), your program should randomly place N points (2N150) inside the square, then draw the net of polygons graphically and color them also randomly. The original N points should be clearly visible.
In the example, buttons read as ``With colors'', ``Polygons'' and ``Quit''.
The source code of your program (i214.pas, i214.cpp, ...) and a short documentation (i214.txt, i214.pdf, ...) should be submitted, also describing your solution and specifying the name of the developer environment to use for compiling.
(10 pont)
Deadline expired on June 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
Minta megoldás:
Englert Péter 12. osztályos (Zalaegerszeg, Zrínyi Miklós Gimnázium) megoldása alapján közöljük.
A négyzet M oldalhosszának, N a pontok számának és a kirajzolás módjának beolvasása után a program véletlenszerű x és y egész koordinátát rendel az (1x,yM) tartományból az N ponthoz (kiemelt pontok).
A KEP tömbben, a négyzet minden pontjához hozzárendeljük annak a kiemelt pontnak az indexét, amelyikhez a legközelebb van (ha többhöz is ugyanolyan közel van, akkor a legkisebb indexűt). A távolságot a megfelelő koordináták különbségeinek négyzetösszegével mérjük; hiszen ennek gyöke Pitagorasz tétele alapján a két pontot összekötő szakasz hossza. Mivel a távolság pozitív érték, ezért a négyzetre emelés nem változtat a sorrendjükön. Az x2 függvény a nemnegatív számokon szigorúan monoton növekvő.
Ha a sokszögek oldalait kívánjuk kirajzolni, akkor a program azokat az (x,y) pontokat rajzolja ki, amelyeknek a 4 közvetlen szomszédja közül legalább egyhez nem ugyanazt a számot rendeltük a KEP változóban (mint az adott ponthoz); vagyis van olyan szomszédja, amelyikhez másik kiemelt pont van legközelebb.
Ha a sokszögeket kiszínezni szeretnénk, akkor a program minden kiemelt ponthoz hozzárendel egy véletlenszerű színt. Utána a KEP tömb alapján minden pontot a hozzá legközelebb álló kiemelt ponthoz tartozó színnel rajzolja ki.
A kiemelt pontok a határvonalak kirajzolása, illetve a színezés után kerülnek megjelenítésre.
Statistics:
5 students sent a solution. 10 points: Balla Attila, Englert Péter, Pap 999 Dávid, Szabó 928 Attila. 1 point: 1 student.
Problems in Information Technology of KöMaL, May 2009