 Problem I. 215. (May 2009)
Problem I. 215. (May 2009)
I. 215. Notice that the following exercise is quite similar to our earlier problem I. 202., this time however you have to use different tools.
We are given some heaps of stones. In every step, we remove one stone from each heap and form a new heap out of these stones. The order of heaps is irrelevant.
In the example, ``A kupacokban a kavicsok száma'' means ``Number of stones in the heaps'', while ``Következő lépésben'' is ``Number of stones in the next step''.

The number of steps can be arbitrary. Since the number of stones is finite, sooner or later the distribution of stones in heaps becomes cyclic.
Prepare a spreadsheet so that the number of stones in each heap can be entered into cells A1:Y1. The following 100 lines should then show the distribution of stones in the next steps. Numbers in each line should be sorted into descending order.
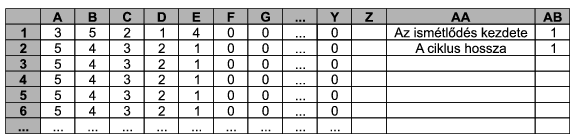
In the table, ``Az ismétlődés kezdete'' means ``Repetition begins at step'' (with the corresponding number in cell AB1), and ``A ciklus hossza'' is ``Length of the cycle'' (to appear in cell AB2).
The total number of stones is at most 25 (you do not have to check this condition). The solution should not use any macros or your own functions.
The sheet (i215.xls, i215.ods, ...) together with a short documentation (i215.txt, i215.pdf, ...) should be submitted, also containing a brief description of your solution and the name of the spreadsheet application.
(10 pont)
Deadline expired on June 15, 2009.
Sorry, the solution is available only in Hungarian. Google translation
A feladat megoldása több részre bontható.
Az egyik lényeges feladat, hogy meghatározzuk a kupacok kavicsszámának sorozatát. A következő kavicssorozat mellékszámításként megkapható minden létező kupac kavicsszámának csökkentésével (A-Y oszlopok a minta számítás munkalapján), valamint egy új, az eredeti kupacok számából adódó kupac létrehozásával (Z oszlop a minta számítás munkalapján). Fontos, hogy az első sorozatot külön kell kezelni, mivel nem volt élhetünk semmilyen feltételezéssel a kupacok sorrendjét illetően. (NAGY függvény)
A következő feladat a számsorozatok kezelhetővé alakítása. Mivel itt 25 elemű tartományokat kellene vizsgálni, a könnyebb kezelhetőség érdekében praktikus ezek tartalmát egyetlen cellatartalommá összefogni. Ennek eredménye a minta ciklus munkalapján látható. (ÖSSZEFŰZ függvény) Voltak, akik nem tagolták szóközökkel számsorozatot. Ebben az esetben ez nem vezet hibához, de nagyobb kavicsszámok esetén nem biztos, hogy igazolható a helyesség.
Végül következik a ciklushossz és az ismétlődéskezdet megállapítása. A mintamegoldásban a ciklus munkalapon a B oszlopban azt vizsgáljuk, hogy az aktuális sorbeli számsorozat hányszor állt elő addig. (DARABTELI függvény)Ha ez a szám nullánál nagyobb, akkor az adott sor tartalmazza az első ismétlődést. A C oszlopban meghatározzuk, hogy az ismétlődő elem hol fordult elő először. (HOL.VAN függvény) Az első előfordulások, azaz a C oszlop értékei közül a legkisebb lesz az ismétlődés kezdete.
Az általunk készített mintamegoldás: minta215.zip
A legtöbb megoldás egyik vagy másik részfeladat leküzdése során egyedi volt. A beküldött megoldások közül Horváth Lóránd megoldását osztjuk meg az érdeklődőkkel: hl215.zip
Statistics:
7 students sent a solution. 10 points: Balla Attila, Horváth 135 Loránd, Kővágó Zoltán, Szabó 928 Attila. 7 points: 2 students. 3 points: 1 student.
Problems in Information Technology of KöMaL, May 2009
