Problem I. 217. (September 2009)

I. 217. A possible model for crystallization is described in this exercise. Suppose that we have N crystallization centres (denoted by black pixels) in a grid of M×M cells containing molten substance (white pixels). Each growing crystal should be coloured differently. Crystallization takes place on the surface of the segregated (coloured) crystal, and crystals grow toward their side neighbours. The growth rate of each crystal is the same: 1 layer in every time step.

The first figure shows a possible grid of crystals after 3 steps.

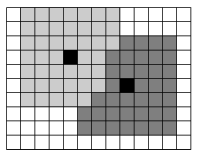
To ensure simultaneous crystallization, we examine all growing crystals in every step, adding a new layer on their surface, if possible. Only molten substance can crystallize, segregated parts no longer change.

You should create a simulation which randomly places N (3N15) crystallization centres on a grid of M×M cells (10M600). Crystals should have random colours, and should grow if there is still molten substance present, otherwise the simulation should stop.

The second figure shows a possible final state.

The source code and project files of your solution (without the .exe file or any other auxiliary files generated by the compiler) should be submitted in a compressed folder (i217.zip).

(10 pont)

Deadline expired on October 12, 2009.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásokról

Több olyan megoldás érkezett, amely formájában nem felelt meg a Versenykiírásnak. A téves állománynév, a tömörítés hiánya, a dokumentáció vagy komment hiánya egy-egy pontveszteséget jelentett.

Horváth 135 Loránd 12. osztályos (Budapest, Németh László Gimnázium) megoldása alapján közöljük:

Ha elképzeljük lépésenként a szimulációt, akkor azt látjuk, hogy a tömbben adva van néhány góc, azaz tömbelem. A tömbelem köré a kristályosodás következő lépésekor keletkezik egy keret. A keret vastagsága megegyezik azzal a számmal, ahányadik lépésnél tartunk.

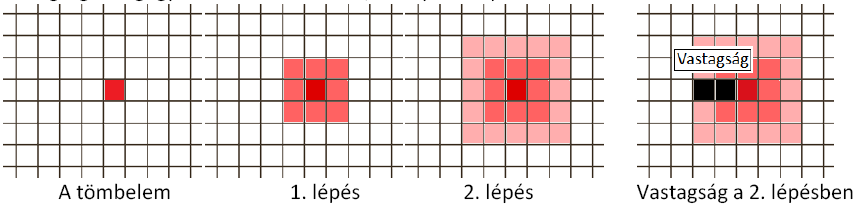
A szimuláció minden lépésében egy ”keretet vonok” a már meglévő rész köré. A tömböt feldolgozás előtt feltöltöttem csupa nullával, ez jelképezi az olvadékot. Ahol már kikristályosodott az anyag, ott nullától eltérő szám van, ami az adott rész színét írja le.

Feldolgozáskor mindig csak abba a tömbelembe írok, ami eddig 0 volt. Így kialakulnak a kristályosodási határok anélkül, hogy valami ”belelógna” a másikba.

A keret rajzolása két lépésből áll: A keret vízszintes részeit, majd a függőleges részeket rajzolom meg egy ciklusban.

Ha az i-edik gócpont koordinátái a goc[i].x és a goc[i].y, akkor a keret felső része az n-edik lépésben a következő lesz:

(goc[i].x-lepes, goc[i].y-lepes) ...(goc[i].x+lepes, goc[i].y-lepes) Például a második lépésben a goc[i].x-2-től a goc[i].x+2-ig kell vonni egy keretet: A szimuláció addig tart, ameddig az összes olvadék ki nem kristályosodik, amíg az olvadek logikai változó értéke hamis nem lesz Ezután kirajzolom a szimuláció eredményét.

Mintamegoldás

Janosov Milán 12. osztályos (Veszprém, Lovassy László Gimnázium) programja i217A.pas

Statistics:

16 students sent a solution.
10 points:	Balla Attila, Barta 111 János, Bostyai Marcell, Fejes Márk, Giczi Dániel, Horváth 135 Loránd, Janosov Milán.
9 points:	Mészöly Dániel Máté, Pap 999 Dávid, Szabó 928 Attila.
8 points:	2 students.
5 points:	1 student.
4 points:	2 students.
2 points:	1 student.

Problems in Information Technology of KöMaL, September 2009