Problem I. 250. (November 2010)

I. 250. We would like to model the spread of cracks on a rectangular plate of size \(\displaystyle N\times M\) (\(\displaystyle 5\le N,M\le 100\)).

First fill the rectangle with random integers between 0 and 99. Cracks will emerge from boundary points having the largest numbers. (If there are more maximal numbers on the boundary, more cracks will be initiated simultaneously.) The direction of the spread of a crack depends on the orientation of the side they were born on: a crack coming from below can spread only upwards, to the left or to the right. If a crack started from the right, it can only move to the left, upwards or downwards. (Cracks coming from the other directions follow a similar rule.)

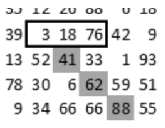
In the first example, the crack started from below. The 3 possible next steps are framed.

The crack will move into the direction determined by the largest of the 3 possible numbers. If there are identical numbers among them, the crack will bifurcate into the corresponding directions. A crack stops, if it reaches the boundary of the rectangle or runs into another already existing crack.

Your program should simulate and show the spread of the cracks on the \(\displaystyle N\times M\) rectangle.

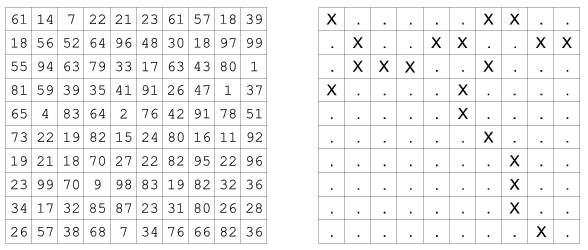
The first two arguments to your program should be \(\displaystyle N\) and \(\displaystyle M\), while the third one should be the name of an output file. The output file should contain the matrix of your random numbers and the cracks similarly to the second example. (Cracks are denoted by ``X'' characters, the other squares contain ``.'' characters. Numbers and these characters should be separated by a space.) This example shows a possible final state on a \(\displaystyle 10\times 10\) rectangle.

The source code (i250.pas, i250.cpp, ...) together with a short documentation (i250.txt, i250.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted in a compressed file (i250.zip).

(10 pont)

Deadline expired on December 10, 2010.

Sorry, the solution is available only in Hungarian. Google translation

Mintamegoldás:

Barta János (Salgótarján, Madách Imre Gimnázium 11. osztály) megoldását közöljük: i250.dpr

Statistics:

7 students sent a solution.
10 points:	Barta 111 János, Gema Barnabás, Hoffmann Áron, Szabó 928 Attila.
8 points:	1 student.
6 points:	1 student.
0 point:	1 student.

Problems in Information Technology of KöMaL, November 2010