 Problem I. 253. (December 2010)
Problem I. 253. (December 2010)
I. 253. In this exercise the last street of a little village is considered. Houses are located only on one side of the street, with each having a painted wooden fence. Each fence has a single color and houses are not directly adjacent to the front fences.
The file utca.txt describes properties of the fences for each house in order: each line of the file contains 2 integers and a word of at most 20 characters. The first number is the length of the front fence in meters (the other dimension of the rectangular house lots is the same in each case), the second number is the distance of the front gate from the corner of the lot. The gate is now considered to be a single point in this model and never touches the common boundary of two lots. The word describes the color of the fence. The length of the street is at most 10 km.
According to the second line of the example, the second house lot in the street has front length of 18 m, and its gate is located 5 m from the corner (therefore the distance between the gate and the end of the street is 20 m).
15 3 sarga
18 5 kek
11 4 sarga
...
Create a program to answer the following questions. The source code of the program should be saved as porta. When writing on the screen, the number of the actual task together with the expected type of the query (e.g. ``Task #4: please enter the distance between the lamp posts'') should be displayed.
1. Read the file utca.txt and then solve the following tasks.
2. Give the number of house lots with red fence.
3. Give the ratio between the largest and smallest area of house lots, to two decimal places.
Street lighting is now being constructed in the village. A lamp post is put on the corner of this street, then the distance between successive lamp posts is given as \(\displaystyle v\) m. Each lamp is capable of illuminating a fixed length of the fences, \(\displaystyle l\) m before and \(\displaystyle l\) m after the lamp post. We know that \(\displaystyle v\) and \(\displaystyle l\) are integers with \(\displaystyle v\ge 2l\), that is, illuminated areas can not be disjoint.
4. Prompt for the values of \(\displaystyle v\) and \(\displaystyle l\). Use these values in tasks below.
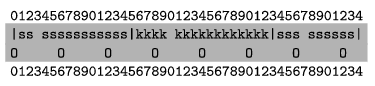
5. Create a map of the street with lamp posts included in the file kep.txt. The first line should contain the fences, the second one the lamp posts. Boundaries are denoted by the ``|'' character, while fences by a space. Each fence is denoted by the starting letter of its color. Lamp posts are marked with ``O''. The example in this task corresponds to the previous example if the distance between lamp posts is 6 m. Your output should only contain the two lines with grey background.
6. In order to minimize costs, if there is nobody on the street, only the minimal number of lamps should be active so that each gate is illuminated. Active lamps should be determined by the following algorithm.
Loop until there is an unilluminated gate
Locate the first such gate
Determine the last lamp which illuminates it
End of loop
The number of active lamps should be displayed and separated by a space.
7. In order to minimize costs even further, a lamp should only be active if there is somebody staying in its light cone. Determine and display the total illumination time (in minutes) if someone walks through the entire street with 100 m/s just along the fences.
The source code (i253.pas, i253.cpp, ...) together with a short documentation (i253.txt, i253.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution--should be submitted in a compressed file (i253.zip).
(10 pont)
Deadline expired on January 10, 2011.
Sorry, the solution is available only in Hungarian. Google translation
A feladatot érettségi feladatnak szántuk, bár egyes elemeiben - úgy látszik - nehéznek bizonyult.
Néhányan plusz munkát is csináltak maguknak, ellenőrizték a bemeneti fájl meglétét, a v és l kapcsolatát.
A beküldők közül többen nem tudták megfelelően kezelni a adatsorok számát közvetlenül meg nem adó bemeneti fájlt. A szövegfájl utolsó értékes adatot tartalmazó sorának végén is sorvégjel kell álljon. Ennek nem megfelelő kezelése később - jellemzően a a 3. feladat megoldása során - hibát eredményezett.
A 2. feladatot mindenki helyesen oldotta meg.
A 3. feladatban figyelni kellett a bevezető szövegre, amely megadta, hogy a telkek csak az utcafronti kiterjedésükben térnek el.
A 4. feladat szövege sajnos tartalmazott egy zavaró részletet, amelyet értelemszerűen lehetett korrigálni: a fénykör sugarának el kell érnie a lámpatávolság felét - különben egyes területek sötétben maradnának. A v és l értékek viszonyát vizsgáló részt kikommenteltem a fordítás előtt, hogy ki tudjam próbálni más értékekre is.
Az 5. feladatot nehezebbnek gondoltuk, de majdnem mindenki sikerrel birkózott meg vele. Aki hibázott, annak is inkább technikai problémája volt, nem a feladat lényegével adódott gondja.
A 6. feladat megoldását a megadott példa nem segítette kellően. Akik kihasználták a már említett plusz feltételt, nem kellett a példaként adott algoritmust kövessék a megoldás során.
Aki a feltételt nem használta ki, annak számára a megadott algoritmusrészlet lényegének követése (nem feltétlen szolgai megvalósítása) azonban fontos volt. Az első bekapcsolt lámpának az első kaput megvilágítók közül a legnagyobb sorszámúnak kell lennie. A mintamegoldás az egymásba lógó fénykörökre - tehát egy kicsit nehezebb feladatra vonatkozik.
A 7. feladatnál majd minden megoldónak nyilvánvaló volt, hogy a a legelső lámpa nem fog annyi ideig égni, mint a második. Az utolsó lámpa kapcsán már kevesebben gondoltak erre. (Ha az említett feltételt nem használjuk ki, akkor több végéhez közeli lámpa fényköre is kívül eshet az utca végén. A mintaként adott megoldás ezt az eshetőséget is figyelembe veszi.)
A beküldött munkák értékelése az eredeti szöveg figyelembe vételével készült. (A korábbi szöveg attól eltérő kiegészítései a feladat későbbi felhasználása miatt érdekesek.)
Rövidített értékelőlap: i253ertekel.pdf
Tesztfájl: utca.txt
Egy lehetséges megoldás - egymásba nyúló fényköröket tartalmazó, tehát a valóságot jobban megközelítő és ezáltal valamivel nehezebb feladatra: i253.cxx
Statistics:
10 students sent a solution. 10 points: Hoffmann Áron, Kompis Ádám, Leitereg András, Paróczi Gergő, Szabó 928 Attila. 9 points: Barta 111 János, Gema Barnabás, Kalló Kristóf, Seres Márk Dániel. 7 points: 1 student.
Problems in Information Technology of KöMaL, December 2010
