 Problem I. 264. (March 2011)
Problem I. 264. (March 2011)
I. 264. According to the ``rounding lemma'', for every matrix with real entries but all row sums and column sums integers, there exists a matrix with integer entries having the same row sums and column sums as the original one, moreover, each element of this integer matrix is the lower or upper integer part of the corresponding element of the original real matrix.
The proof of the rounding lemma is quite straightforward and also gives an algorithm how to construct the integer matrix.
If the original matrix has only integer entries, then we are done. Otherwise pick a non-integer element. Since the row sums are integers, there exists another non-integer number in the same row. But column sums are also integers, so the column of this second element must contain a third non-integer, whose row contains a fourth non-integer, and so on.
By alternately selecting rows and columns and marking the corresponding non-integer elements, sooner or later we have to visit a row or column that has already been selected. In this row or column there are exactly two matrix elements marked in an earlier stage, the element marked first is denoted by \(\displaystyle x\), while the element marked second is denoted by \(\displaystyle z\). Of course, there is a third element in this row or column, denoted by \(\displaystyle p\), which has been marked last, due to which we revisited the actual row or column. (In may happen that \(\displaystyle p=x\).)
Let us consider now the walk of this graph after we found \(\displaystyle p\). This walk begins with \(\displaystyle z\) and ends in \(\displaystyle p\), see the example. It is easily seen that the length of this walk is even, and contains exactly two marked matrix elements successively of each affected row or column. Therefore we can alternately add and subtract a constant \(\displaystyle \delta\) from the successive elements of this walk without changing any of the row or column sums.
Example. Suppose we start from the top left corner and visit non-integer elements in the order \(\displaystyle a_{11}\), \(\displaystyle a_{14}\), \(\displaystyle a_{34}\), \(\displaystyle a_{32}\), \(\displaystyle a_{12}\). After the \(\displaystyle 4^{\rm th}\) step (\(\displaystyle p =a_{12}\)) we reach a row already visited earlier (\(\displaystyle x=a_{11}\), \(\displaystyle z=a_{14}\)). The walk described in the above paragraph is therefore \(\displaystyle a_{14}\), \(\displaystyle a_{34}\), \(\displaystyle a_{32}\), \(\displaystyle a_{12}\).
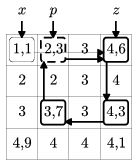
This constant \(\displaystyle \delta\) is defined to be the minimal (signed) distance between the marked matrix elements and the corresponding nearest integers. Then no ``overflow'' can occur when \(\displaystyle \delta\) is added or subtracted: each affected matrix element is changed at most to its lower or upper integer part and the number of non-integer elements is decreased by at least one.
Finally, the whole procedure is repeated if there are still non-integer elements in the matrix.
You should create a spreadsheet to perform a single iteration step of the above algorithm. The input and output matrix, further the constant \(\displaystyle \delta\) should be displayed similarly to our figure. (In the example, ``Bemenet'' is the input, ``Kimenet'' is the output, while ``Delta értéke'' is the value of \(\displaystyle \delta\).) Your sheet should be able to handle matrices of size at least \(\displaystyle 10\times 10\). Marked matrix elements should be displayed by using conditional formatting in both matrices. You can display an arbitrary solution if there is more than one.
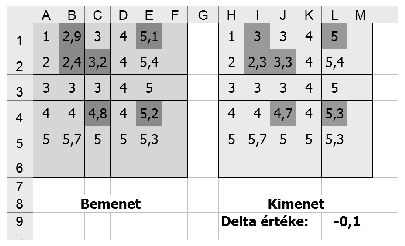
The task should be solved by using spreadsheet functions and without any macros. Auxiliary computations should be described in detail.
The spreadsheet (i264.xls, i264.ods, ...) together with a short documentation (i264.txt, i264.pdf, ...) describing your solution and the name and version number of the spreadsheet application should be submitted.
(10 pont)
Deadline expired on April 11, 2011.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás
Mintamegoldásként közöljük Szabó Attila (Pécs, Leőwey Klára Gimn.) munkáját, amely OpenOffice 2.1-gyel készült.
Statistics:
4 students sent a solution. 10 points: Szabó 928 Attila. 7 points: 1 student. 5 points: 1 student. 2 points: 1 student.
Problems in Information Technology of KöMaL, March 2011
