Problem I. 274. (October 2011)

I. 274. We are given an n×m rectangular grid (1n,m500) consisting of black and white squares. Your task is to locate the rectangle with maximal area containing only white cells. Coordinates of the upper left and lower right corners together with the area of the rectangle should be given as an output.

In the ``Példa'' example, ``A legnagyobb téglalap'' is ``the largest rectangle'', and ``Területe'' is ``with area''.

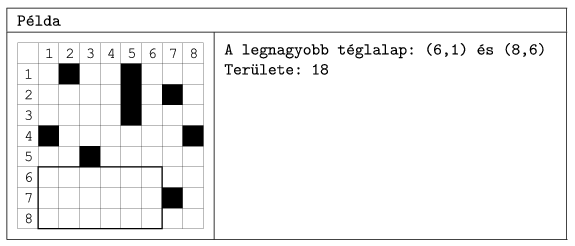
For the solution, you may consider the following method for relatively small values of n and m: by using nested loops, test all possible rectangles given by coordinate pairs whether they contain any black cells, then select the rectangle with maximal area. However, the running time of this algorithm is high when the number of elements is increased, because the number of comparisons is proportional to the 4th power of the number of elements.

So the following hint may be useful: compute and store for each cell the number of black cells in the rectangle with lower right corner being the actual cell.

The table ``A fenti példához számolt értékek'' shows these numbers corresponding to the above example.

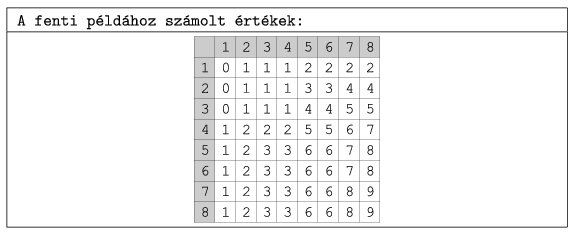
By using these values, the number of black cells in a rectangle given by two coordinate pairs can be determined without loops.

Your program i274 should find the largest rectangle containing only white cells.

The size of the grid and the colors of the cells (0: white, 1: black) are contained in the input file. The first line of this file gives the number of rows (n) and the number of columns (m). Then each of the following n lines contains m values (without spaces) and describes the state of each cell (0 or 1).

The result, that is the upper left and lower right coordinates of the maximal rectangle together with its area, should be displayed on the screen. The only command line argument to your program is the name of the input file. The total running time of your program should be less than 60 seconds on a 2.40 GHz, Core2Duo computer.

In the last table, ``Példa a bemenetre'' is a sample input, while ``Kimenet'' is the corresponding output.

The source code (i274.pas, i274.cpp, ...) together with a short documentation of your program and solution (i274.txt, i274.pdf, ...) -- also specifying the name of the developer environment to use for compiling the source file -- should be submitted in a compressed file i274.zip.

(10 pont)

Deadline expired on November 10, 2011.

Sorry, the solution is available only in Hungarian. Google translation

Megoldásokról:

Viszonylag sok, teljes értékű megoldás érkezett. A megoldók egy része nem használta a feladat szövegében megfogalmazott ötletet, hogy előre számítsuk ki és tároljuk el minden cellához, hogy a terület bal felső sarkával együtt téglalapot alkotva hány fekete cellát tartalmaz. Az így előkészített értékekkel két koordináta-párral megadott téglalap fekete cella-tartalma ciklusok nélkül kiszámítható.

Többen észrevették, hogy az egyes cellákhoz tartozó fekete négyzetek számát rekurzív módszerrel meg lehet határozni:

Ha (a,b) cella fekete, akkor T(a,b)=T(a-1,b)+T(a,b-1)-T(a-1,b-1)+1. Ha a cella fehér, akkor T(a,b)=T(a-1,b)+T(a,b-1)-T(a-1,b-1).

A T(0,b)=0 és T(a,0)=0, minden a-ra és b-re.

Ha egy téglalap bal felső sarka (a1,b1) és a jobb alsó sarka (a2,b2) és nincs benne fekete cella, akkor: T(a2,b2)=T(a1-1,b2)+T(a2,b1-1)-T(a1-1,b1-1). Az algoritmus egymásba ágyazott ciklusok segítségével mindig egy adott cellából kiinduló téglalapokat vizsgálja, majd a nem fekete cella tartalmúak közül a legnagyobbat választja ki.

Mintamegoldásként Szilágyi Dániel 10. osztályos (Újvidék, Jovan Jovanovic Zmaj Gimnázium) tanuló munkáját közöljük: I274.cpp

A megoldások vizsgálatához használt tesztállományok: teszt.zip

A tesztállományok nevei, egyik legnagyobb téglalap két koordinátája, amely csak fehér cellákat tartalmaz és ennek területe:

Statistics:

12 students sent a solution.
10 points:	Adrián Patrik, Antal János Benjamin, Barkaszi Richárd Miklós, Fényes Balázs, Gema Barnabás, Hoffmann Áron, Jákli Aida Karolina, Kovács Balázs Marcell, Kucsma Levente István.
9 points:	Varga 256 Erik.
8 points:	1 student.
5 points:	1 student.

Problems in Information Technology of KöMaL, October 2011