 Problem I. 292. (April 2012)
Problem I. 292. (April 2012)
I. 292. In this exercise you are going to simulate the path of a robot moving on a huge grid. In each step the robot advances one unit parallel to one of the coordinate axes. The robot starts from point (0,0) and executes a predefined series of steps consisting of letters E, H, J and B. Suppose that the current position of the robot is (x,y), then command E (forward) will move the robot to (x,y+1), command H (back) to (x,y-1), command J (right) to (x+1,y), and command B (left) to point (x-1,y).
The grid contains some checkpoints. After each step the robot records the sum of distances from the checkpoints. The distance of two points is now the Manhattan distance, for points (x1,y1) and (x2,y2) it is defined as |x1-x2|+|y1-y2|.
The first command line argument to your program is the name of an input file containing the necessary data. The first line of this file contains the number of checkpoints N () and the number of steps M (
). The following N lines then contain the x and y coordinates of the checkpoints (
) separated by a space. There can be some checkpoints having both coordinates equal. The next line finally contains M characters (E, H, J or B) describing the steps of the robot.
The second command line argument to your program is the name of the output file. It should have M lines, each containing an integer, being the above sum of distances after each step.
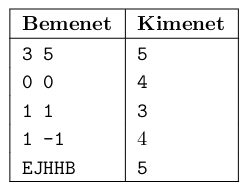
In the example, Bemenet is the input and Kimenet is the corresponding output.
Your program should solve the task within 1 second. Due to the high number of grid points and checkpoints, it may be useful to make appropriate preparations before computing the sum of distances to improve the efficiency of your program.
The source code (i292.pas, i292.cpp, ...) together with a short documentation (i292.txt, i292.pdf, ...) -- also describing which developer environment to use for compiling, further a brief description of your solution -- should be submitted.
Based on a problem of Adrian Satja Kurdija, Croatian Open Competition in Informatics
(10 pont)
Deadline expired on May 10, 2012.
Sorry, the solution is available only in Hungarian. Google translation
Megoldásokról:
A beküldött programok egy része minden robotlépés után az összes ellenőrzési pont távolságának összegét újraszámolta. Ezzel a módszerrel a futási idő legfeljebb 1-2000 ellenőrzési pontig és 1-2000 robotlépésig lesz 1 másodperc alatt. Ha az értékek ennél nagyobbak, akkor előfeldolgozást érdemes végezni. Ennek egy lehetséges módszerét Antal János Benjamin (Nyíregyháza, Széchenyi István Közgazdasági Szakközépiskola)12. osztályos tanuló adta meg:
Az adatok beolvasása után feltöltöm a függőleges és vízszintes tömböket. A függőleges tömb i. eleme először azt tartalmazza, hogy hány olyan pont van, amelynek y koordinátája pontosan i. A következő lépésben a függőleges tömb i-dik eleméhez hozzáadok az (i-1). elemet. Így a függőleges tömb azt fogja tárolni, hogy az y=i egyenesen és az alatt hány darab pont van. A vízszintes tömb hasonló lépéseken megy keresztül, csak az x koordinátával, és végül azt fogja tárolni a tömb i. eleme, hogy az x=i egyenesen és attól balra hány pont található. Ez azért fontos, mert a rács bármely részén áll a robot, egy tömbindexeléssel meg lehet mondani, hány pont van tőle balra/jobbra vagy felfelé/lefelé. Ezután megszámolom az összes ellenőrzőpont és a robot távolságát. Minden lépés után csak a következőket csinálom, akár E/H/J/B lépés volt, mindig megnézem a függőleges vagy vízszintes tömb segítségével, hogy a robot lépésének irányában hány pont van a robottól abban az irányban. Ezt a darabszámot kivonom az össztávolságból, mert mindegyik ponthoz 1 egységgel közelebb került. Utána ezt a darabszámot kivonom az N-ből, így megkapom hány ponttól távolodott pontosan 1 egységet. Ezt hozzáadom az össztávolsághoz, és meg is van a lépés utáni távolságok összege anélkül, hogy végig kellett volna számolni az összes pont távolságát.
Mintamegoldása: i292.pas
Tesztállományok: tesztallomanyok.zip
Statistics:
12 students sent a solution. 10 points: Antal János Benjamin, Jákli Aida Karolina, Kucsma Levente István, Varga 256 Erik. 8 points: 1 student. 7 points: 3 students. 6 points: 2 students. 5 points: 2 students.
Problems in Information Technology of KöMaL, April 2012
