Problem I. 294. (April 2012)

I. 294. Lissajous curves are obtained if we trace the path of a point mass influenced by two perpendicular oscillations. These curves can have intricate shapes depending on the choice of the parameters. 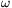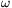To describe these curves in Cartesian coordinates, we let $x(t)=A_1 \sin\, (\omega_1 t+\varphi_1)$ and $y(t)=A_2 \sin\, (\omega_2 t+\varphi_2)$ , where x(t) and y(t) are the two coordinates of the point as functions of time, A₁ and A₂ are the amplitudes, $\omega$ ₁ and $\omega$ ₂ are the angular frequencies, finally, $\varphi$ ₁ and $\varphi$ ₂ are the phase angles corresponding to time t=0.

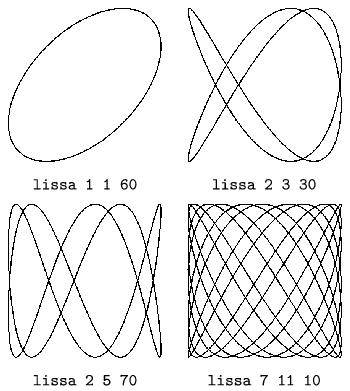
You should create a Logo procedure to display the orbit of the point. For simplicity, we fix A₁=A₂=400 pixels and $\varphi$ ₁=0.

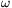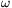The name and parameters of your procedure should be lissa o1 o2 fi2, where o1, o2 and fi2 are the values of $\omega$ ₁, $\omega$ ₂ and $\varphi$ ₂.

The Logo project file (i294.imp, i294.lgp) containing the procedure, together with a short documentation (i294.txt, i294.pdf, ...) and the name of the program you have used should be submitted.

(10 pont)

Deadline expired on May 10, 2012.

Sorry, the solution is available only in Hungarian. Google translation

Lényegében mindenki jól ragadta meg a feladatot. sok szép rekurzív megoldás született. Általánosságban elmondható, hogy a rekurziónál kisebb lépésközzel lett volna célszerű dolgozni, hogy a görbe tényleg görbe lehessen nagy értékű paraméterek esetén is, bár volt, aki ezt is ügyesen megoldotta. Mintaként ajánlom Gema Barnabás (Veszprém, Lovassy László Gimnázium) egyszerűségében szép, hibátlan megoldását. i294.IMP

Statistics:

7 students sent a solution.

10 points: Gema Barnabás.

9 points: Fényes Balázs, Kovács Balázs Marcell.

8 points: 2 students.

7 points: 2 students.

Problems in Information Technology of KöMaL, April 2012

7 students sent a solution.
10 points:	Gema Barnabás.
9 points:	Fényes Balázs, Kovács Balázs Marcell.
8 points:	2 students.
7 points:	2 students.

Already signed up?
New to KöMaL?