Problem I. 311. (January 2013)

I. 311. Concrete paver blocks are laid by a machine in a park. The park is rectangle-shaped and the blocks are squares of unit side length. The machine can move forward, backward, right or left, by one unit, in each step. In each step a block is laid. During the construction, the path may cross itself. In this case, blocks are placed on top of one another. These extra blocks should be collected and removed later.

The path of the machine is described in advance in a file as a coordinate sequence of horizontal and vertical units. Each line of the file (3N100) contains the actual x and y coordinates of the machine. The machine can start from any grid point of the park and it can lay at most 200 blocks in one run.

By using a spreadsheet application, you should solve the following tasks. The solution should not use any macros or own functions.

1. Beginning with cell A1, import the UTF-8 encoded, tabulator separated text file utterv.txt (downloadable from our site), and save the sheet as i311 in the default format of the spreadsheet application.

2. By inserting rows and columns, and filling up cells, create a header similar to the sample.

3. The path of the machine and the laid blocks should also be displayed by using characters. To achieve this, first you should adjust the corresponding column widths and row heights such that cells to be displayed appear as squares. Then, row and column coordinates should be shown in bold face.

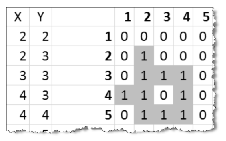
4. By using a copyable formula, you should determine the number of blocks placed on top of one another at each point of the park after the program of the machine has been executed. You may create auxiliary computations in any column, but these should not be hidden.

5. By using conditional formatting and coloring the cells, you should highlight the path of the machine. You should rename the sheet to Terkep (``map'').

6. Create a new sheet Elemzes (``analysis''). The following tasks should be answered in this sheet. Auxiliary computations are allowed in any column, and, similarly as before, these should also remain visible.

7. Compute how many percent of the area of the park is not covered with blocks.

8. What is the maximal number of blocks put on top of one another? What are the coordinates of this square? (If the answer is not unique, you can freely choose one to give.)

9. For each of the 4 edges of the park, determine the coordinates of the block which is located the closest to the actual edge. (If there are more blocks with the smallest distance, it is sufficient to give one of them.)

10. How many blocks should be removed finally such that no overlaps remain?

11. If the above extra blocks can be removed and transferred to the square with coordinates (0,0) located outside the park only one by one, then what is the total path length covered during this operation? (We assume now that, when carrying a block, only steps to the left and up are allowed.)

Your spreadsheet (i311.xls, i311.ods, ...) together with a short documentation (i311.txt, i311.pdf, ...) - also describing the name and version number of the spreadsheet application - should be submitted.

Downloadable file: utterv.txt

(10 pont)

Deadline expired on February 11, 2013.

Sorry, the solution is available only in Hungarian. Google translation

Mintamegoldás:

Qian Lívia 10. évfolyamos tanuló (Szeged, SZTE Ságvári Endre Gyakorló Gimnázium) megoldását közöljük: i311.xlsx

Statistics:

8 students sent a solution.
10 points:	Fényes Balázs, Gema Barnabás, Qian Lívia.
9 points:	Jákli Aida Karolina, Kalló Kristóf, Tomku György.
8 points:	1 student.
7 points:	1 student.

Problems in Information Technology of KöMaL, January 2013