 Problem I. 335. (December 2013)
Problem I. 335. (December 2013)
I. 335. There are several popular tabletop games for every age group: the simplest version of Super Six dice game we discuss here is a relatively new game, based on pure chance.

The rules of the game are the following. First, every player gets the same number of wooden sticks. Then a starting player is selected, and players roll a die one after another in a clockwise direction. There is a little cylinder in the game with holes numbered from 1 to 6 on its top: the current player can put one of their sticks into a hole provided that the die shows that number and the hole is still empty. If that hole has already been filled earlier, the player gets the actual stick from the hole. Six is a special number in the game, because its corresponding hole is different: a stick put into hole ``6'' falls into the cylinder and stays there until the end of the game. After rolling a ``6'', the player can roll again. The winner is who first gets rid of their sticks. (The other version of Super Six as a logic game is played with two dice and different rules.)
You should simulate the above game in a spreadsheet application and save the board in the default file format of the application named as i335.
In your solution, you should take into account the following.
- Try and use formulas, functions or references, but your own functions and any macros should not be used.
- Auxiliary computations can be performed to the right of column M, but explanatory comments should be added.
The game is now played by 3 players (``Játékos'' in the example), Anna, Blanka and Csaba. Their names should be placed in cells C3:E3. The initial number of sticks (3-9 pieces) is to be put in the cells directly beneath the corresponding player's name.
Cell B2 should contain the name of the starting player (``Kezdő''). The game simulation is to be found below the 4th row. For each turn, columns G:L should contain the distribution of the empty or filled holes on the top of the cylinder, and the number of sticks in the cylinder. Empty holes are depicted by lighter cells, whereas filled holes by darker ones.
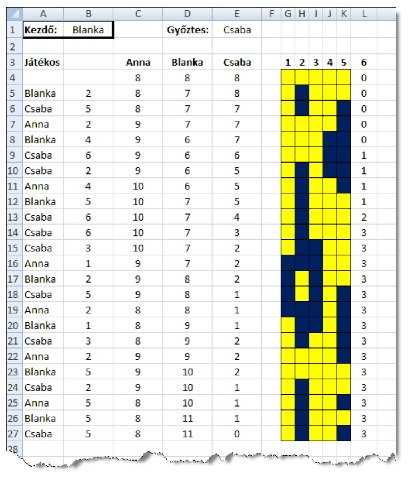
Column B should contain the random integers corresponding to the numbers on the die in each turn, while cells below A5 contain the name of the next player according to the rules. Cells C:E should have the number of sticks for each player in each turn.
The simulation of the successive turns should continue until there is a winner. Your sheet should be able to simulate the game for 100 turns. Cells in the winning position should appear as empty ones. The name of the winner should be displayed in cell E1. A warning can be issued in cell E1, in the rare case when there is no winner in the first 100 turns.
The spreadsheet (i335.xls, i335.ods, ...) together with a short documentation (i335.txt, i335.pdf, ...) also describing your solution, and the name and version number of the spreadsheet application should be submitted in a compressed file (i335.zip).
(10 pont)
Deadline expired on January 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
A megoldásról:
Kovács Balázs Marcell, 11. évfolyamos tanuló (Budapest, ELTE Radnóti Miklós Gyakorló Iskola) munkája:
Az O oszlopban tároljuk a soron következő játékos sorszámát, a következő játékos az előző játékos sorszámának 3-mal való osztás maradékával van meghatározva (ha a dobás nem 6).
Az első játékos sorszámát a MATCH() függvény segítségével határozzuk meg.
A P oszlopban tároljuk, hogy az adott körben tart-e még a játék (1: igen, 0: nem). Az 1-es érték feltétele, hogy legyen minden játékosnak min. 1 pálcája, valamint hogy az előző körben is tartson a játék. A P oszlop értékei alapján dől el, hogy az A-E, valamint az L oszlopokban megjelenítünk-e valamit.
Az R-W oszlopok tartalmazzák, hogy az egyes lyukakban hány pálcika van. Új körben ezek az értékek a dobott szám alapján változnak, a 6-os oszlop mindig 1-gyel nő, a többi 0-ról 1-re, 1-ről 0-ra vált (1-előző). A G-K oszlopban ezen értékek alapján van megvalósítva a színezés conditional formatting-gal.
Az Y-AA oszlopban található, hogy az egyes játékosoknál hány pálcika van. Egy az egyben ez van megjelenítve a C-E oszlopokban is. 6-os dobás esetén 1-gyel csökken az érték, különben pedig az adott lyuk előző köri állapotától függően 1-gyel nő, vagy csökken.
A P1 mezőben meghatározzuk, hogy hány körből állt a játék, ez alapján jelenítjük meg az utolsó játékos nevét az E1 cellában, ha nincs nyertes, akkor P1=101 (a játék menetét 101 körön keresztül követjük, mert előfordulhat, hogy éppen a 100. körben nyer valaki), akkor az E1 cellában a NINCS felirat jelenik meg.
Statistics:
17 students sent a solution. 10 points: Bognár 2012 Balázs, Fényes Balázs, Gercsó Márk, Kelkó Balázs, Kovács 246 Benedek, Kovács Balázs Marcell, Mócsy Miklós, Németh 123 Balázs, Németh 729 Gábor, Radnai Bálint, Szabó 524 Tímea, Tegzes Tamás. 9 points: Uzonyi 000 Ákos. 8 points: 2 students. 4 points: 2 students.
Problems in Information Technology of KöMaL, December 2013
