 Problem I. 346. (April 2014)
Problem I. 346. (April 2014)
I. 346. The present exercise is similar to our earlier Problem I. 343. Now we again have an \(\displaystyle N\times N\) (\(\displaystyle 4\le N\le 50\)) board, and each cell of the board is either empty or has some color. When the board is in its vertical position, the colored squares try to occupy the lowest possible empty positions due to the gravitational force. This time however the board also contains some preset and fixed obstacles that block the way of the sliding colored squares. Empty squares are denoted by a . character, the colored squares can be either red (denoted by P), blue (K) or green (Z), while a fixed obstacle is denoted by A. The board is surrounded by a border preventing the colored squares from falling out. In this exercise the board can be rotated only to the right. After the rotation, the colored squares will again slide to the lowest free positions, and they will stay on top of each other. We are now interested in the mixing effect due to the presence of the obstacles and the rotations. In the example, ``indulás'' is the starting position, and ``1. forgatás után'' is the state of the board after the first right turn.
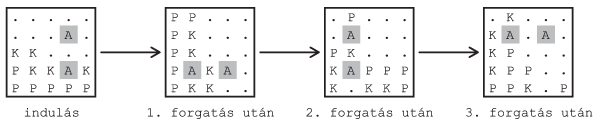
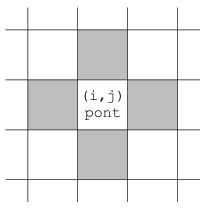
In the starting position and after each rotation you should determine the number of colored squares having at least two neighbors of the same color. The figure shows that a square \(\displaystyle (i,j)\) has by definition 4 neighbors.
Create your program i346 to simulate the rotation of the board and the mixing of the colors.
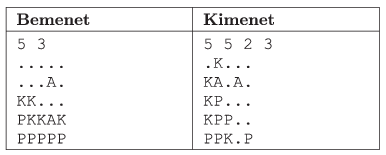
The first command line argument to your program is the name of the data file describing the board. The first line of the file contains the board size \(\displaystyle N\) (\(\displaystyle 4\le N\le 50\)) and the number of rotations \(\displaystyle K\) (\(\displaystyle 1\le K\le 100\)). The following \(\displaystyle N\) lines contain the initial cell content of the board.
The second command line argument to your program is the name of the output file. The first line of this file should contain the number of colored squares having at least two neighbors of the same color after each rotation; these numbers should be separated by a space. The remaining \(\displaystyle N\) lines of the output file should describe the content of each cell of the board after the last rotation; each line of the file corresponds to a row of the board. In the example, ``Bemenet'' is an input, while ``Kimenet'' is the corresponding output.
The source code (i346.pas, i346.cpp, ...) of your program and a brief documentation (i346.txt, i346.pdf, ...) of your solution should be submitted, also specifying the name of the developer environment to use for compiling your source.
(10 pont)
Deadline expired on May 12, 2014.
Sorry, the solution is available only in Hungarian. Google translation
A kimeneti fájl első sorába a forgatások számánál eggyel több számot ír a program. Az első szám a kezdeti állapotot mutatja. Sajnos egy kis elírás történt a lapban és a minta bemenetre ez az első érték nem 5 a kimenetben, hanem 6.
Tesztállományok: tesztbe.zip teszteredmenyek.ki
Minta megoldás:
Paulovics Zoltán 11. osztályos tanuló (Zrínyi Miklós Gimnázium, Zalaegerszeg) megoldása: i346.vb
Statistics:
12 students sent a solution. 10 points: Csernák Tamás, Fényes Balázs, Kovács 246 Benedek, Kovács Balázs Marcell, Paulovics Zoltán, Radnai Bálint, Uzonyi 000 Ákos. 8 points: 2 students. 5 points: 2 students. Unfair, not evaluated: 1 solutions.
Problems in Information Technology of KöMaL, April 2014
