 Problem I. 349. (May 2014)
Problem I. 349. (May 2014)
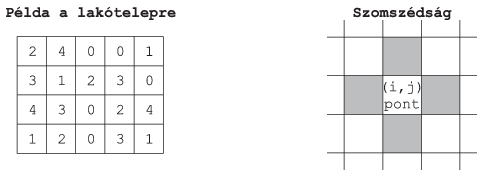
I. 349. The first figure of this exercise shows a rectangular area consisting of \(\displaystyle N\times M\) (\(\displaystyle 2\le N,M\le 50\)) tower blocks viewed from above. The horizontal cross sections of the towers are identical squares. The number of levels of a tower block varies between 1 and 9; the value 0 denotes a square-shaped park area. The figure ``Szomszédság'' (neighborhood) shows that a particular square has 4 neighboring squares by definition. On each level of each tower block there is exactly one flat.
Create your program i349 to answer the following questions by using data from the file telep.txt. Before writing any result to the screen, the number of the actual task (for example, Task #3:) should be displayed. If the user is prompted to enter any data, then the type of this requested input should also be shown. Diacritical marks in the output may be omitted.
The first line of the file telep.txt contains the values of \(\displaystyle N\) and \(\displaystyle M\). The following \(\displaystyle N\) lines describe the number of levels of each tower block or the parks, see the example.
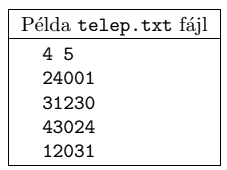
1. Read the data from the file telep.txt to solve the following tasks.
2. Determine and display to 2 decimal digits the percentage of the park area relative to the total area.
3. The view from a window is important to many people. By definition, one can see out of a window of a given flat in a particular direction (vertical or horizontal, if viewed from above) as long as the neighboring flats are lower than the actual one. Display the number of flats with the property that there is a (vertical or horizontal) direction such the border of the rectangular area occupied by the tower blocks can be seen from that window of the flat.
4. Some customers are interested not only in the view, but also in being close to a park area or to the border of the rectangular area. Prompt a user to enter a level number, then display the total number of flats on that level with the property that one has a view in some direction, and how many of these flats are adjacent to a park square or the rectangle border. The result should be displayed in the following format:
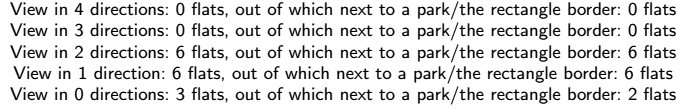
5. From an architectural point of view, the visibility of the whole set of tower blocks is also important. For each row and column of the rectangle, you should determine the number of visible tower blocks if viewed from the east or west directions (for rows), or from the north or south directions (for columns). A tower block is obscured by another tower block of the same size or higher. The results should be written to the file latvany.txt in the following format:
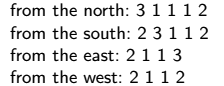
6. Some people would like to live close to a large park area. Read the position of a square in a (row, column) format relative to the top left corner of the rectangle, and display whether there is a park there. If yes, give the number of squares the park occupies.
The source code (i349.pas, i349.cpp, ...) of your program and a brief documentation (i349.txt, i349.pdf, ...) of your solution should be submitted, also specifying the name of the developer environment to use for compiling your source.
(10 pont)
Deadline expired on June 10, 2014.
Sorry, the solution is available only in Hungarian. Google translation
Minta megoldás:
Csernák Tamás 12. osztályos tanuló (Fazekas Mihály Fővárosi Gyakorló Gimnázium, Budapest) megoldása: i349.pas
Tesztállomány: telep.txt
Statistics:
12 students sent a solution. 10 points: Csernák Tamás, Fényes Balázs, Gercsó Márk, Kovács Balázs Marcell, Uzonyi 000 Ákos. 8 points: 3 students. 6 points: 2 students. 5 points: 1 student. Unfair, not evaluated: 1 solutions.
Problems in Information Technology of KöMaL, May 2014
