 Problem I. 353. (September 2014)
Problem I. 353. (September 2014)
I. 353. The game ``Egyszámjáték'' (The Smallest Number Wins Game) was invented by the Hungarian mathematician and psychologist László Mérő: in this game each player submits a positive integer between 1 and 10000, and these numbers are collected. Numbers that have been submitted more than once are deleted. The smallest number among the remaining ones wins.
Example. Players submit the following numbers: 9, 6, 3, 7, 4, 6, 1, 6, 8, 1, 6, 5, 7, 9, 4, 2. We then remove duplicated elements. The remaining numbers are: 3, 8, 5. The player who submitted the smallest such number (3) wins.
Prepare a sheet to evaluate the game based on the numbers submitted by players in email, and to determine the winner. The file tippek.txt (UTF-8 encoded and downloadable from our web page) contains the data for players and the numbers they submitted. For each player we have the following data:
Tipp The integer submitted by the player, \(\displaystyle 1\le \mathsf{tipp}\le 10\;000\);
Név The player's name (there can be more players with the same name);
E-mail The email address of the player, this address is unique.
If there are multiple submissions from the same email address, then only the first submission is taken into account (``valid'') and the others are considered as invalid. You should use a spreadsheet application to solve the following tasks, but user-defined functions or macros cannot be used.
Open the tabulator-separated text file tippek.txt in the application according to the example. It is enough if your solution handles the data given in this file correctly. Your work should be saved as i353 in the default application file format. You should format the sheet according to the example, and give your answers in the cells adjacent to the messages in columns D:G by using expressions. Auxiliary computations can be performed in cells to the right of column H.
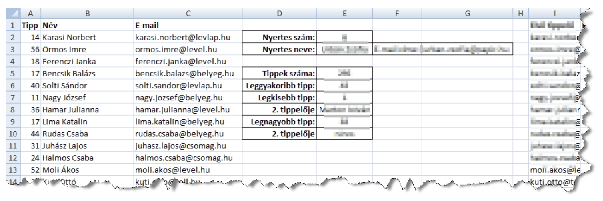
1. The winning number (``Nyertes szám'') should appear in cell E2.
2. The name and email address of the winner (``Nyertes neve'') should appear in cells E3 and G3, respectively.
In the following tasks you should determine some other values and numbers.
3. In cell E5 determine the number of valid submissions (``Tippek száma'').
4. By using a function, determine in cell E6 the number that has been validly submitted the most often (``Leggyakoribb tipp''). If there are multiple such numbers, give only one instance.
5. By using a function, determine in cells E7 and E9 the smallest and the largest valid numbers submitted (``Legkisebb tipp'' and ``Legnagyobb tipp'').
6. In cells E8 and E10, respectively, display the player names (``2. tippelője'') who submitted the smallest and the largest valid numbers for the second time. If there is no second submitter, the message ``nincs'' (= none) should appear.
7. You should format the sheet according to the example.
The spreadsheet (i353.xls, i353.ods, ...) together with a short documentation (i353.txt, i353.pdf, ...) describing the name and version number of the spreadsheet application should be submitted in a compressed file (i353.zip).
Downloadable file: tippek.txt
(10 pont)
Deadline expired on October 10, 2014.
Statistics:
24 students sent a solution. 10 points: Dombai Tamás, Géczi Dániel, Gercsó Márk, Kiss 107 Ádám, Kovács 246 Benedek, Kovács Balázs Marcell, Mócsy Miklós, Piller Trisztán, Radnai Bálint, Tóth Márk Andor. 9 points: Bálint Martin, Fényes Balázs, Kelkó Balázs, Lencsés Ádám, Németh 729 Gábor, Olexó Gergely, Szabó 524 Tímea. 8 points: 3 students. 7 points: 1 student. 6 points: 1 student. 5 points: 1 student. 4 points: 1 student.
Problems in Information Technology of KöMaL, September 2014
