 Problem I. 380. (September 2015)
Problem I. 380. (September 2015)
I. 380. By using a spreadsheet application it is easy to determine the day of the week for a given date. However, many of these applications cannot interpret dates before 1900 January 1. To handle this situation we can use perpetual calendars that were developed in the pre-computer era. Our perpetual calendar has 3 auxiliary tables. The first auxiliary table (``Évek indexszámai'' in the example) assigns an integer (called index) to each year. The second table (``Hónapok kulcsszámai'' in the example) yields another number (called key) based on the index and the number of the month. Finally, by using the third table (``A kapott számértékhez rendelt nap'' in the example) we find the day of the week from the sum of the key and the number of the day of the month (in the examples, ``Héfő'' is Monday, and ``Szombat'' is Saturday). Let us consider 1848 March 15, for example. The index corresponding to 1848 is 45. The key corresponding to 45 and March is 2. Finally, looking up the sum \(\displaystyle 2+15\) in the third table we get Wednesday.
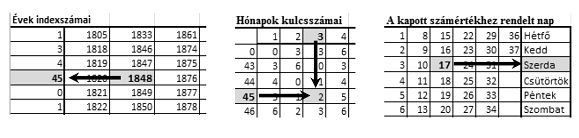
In this task you should create a spreadsheet to find the day of the week for a given date. The auxiliary tables are available to you in the (UTF-encoded and tabulator-separated) file tablak.txt.
1. Read the data file tablak.txt to a sheet beginning with cell A1, then save this sheet as oroknaptar in the default application file format.
2. Now you determine the index corresponding to the given year in two steps. First display-in the cells of row 36 and by using a formula-the row number in which the year (=``Év'') given in cell C1 appears for each of the columns of the auxiliary table B5:T35. If the year does not appear in a particular column, the corresponding cell in row 36 should contain a 0.
3. As a next step, display-in cell C2 and by using a function-the index of the year in cell C1. The index is found in column A5:A35; its row number is specified by the non-zero element of row 36.
4. Next determine the key (=``Kulcs'') and display it in cell E2. The key depends on the index computed above and on the number of the month (=``Hónap'') given in cell E1. The key should be determined by using the table A39:M53 and applying a function: columns of this auxiliary table correspond to the months (B39:M39), while rows correspond to the indices (A40:A53).
5. To determine the day (=``Nap''), display-in cell G2 and by using a formula-the sum of the key (E2) and the number of the day (G1).
6. In the last step, determine the name of the day. Locate the sum computed in G2 by using a formula in the auxiliary table A57:G63: the name of the day-to be displayed in cell I2-is found in the last column of this table in the row in which the sum appears.
7. Each of the 3 auxiliary tables (A5:T35, A39:M53, A57:G63) should be bordered by thin lines inside and thick lines outside. The content of the 3 cells specifying the date, and that of the cell containing the name of the day should appear in bold with light gray background.
8. By using conditional formatting with bold fonts and dark red color, you should highlight
\(\displaystyle a)\) the year in the range B5:T35 that appears in cell C1,
\(\displaystyle b)\) the month in the column header B39:M39 that appears in cell E1,
\(\displaystyle c)\) the index in the row header A40:A53 that appears in cell C2, and
\(\displaystyle d)\) the integer in the range B40:M53 that appears in cell G2 (as ``Számérték'').
Downloaded file: tablak.txt.
Sample:
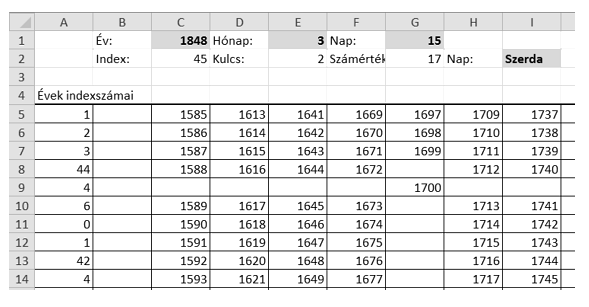
You should submit your sheet and a short documentation in a compressed file i380.zip.
(10 pont)
Deadline expired on October 12, 2015.
Statistics:
13 students sent a solution. 10 points: Hamrik Szabin, Kelkó Balázs, Kovács 246 Benedek, Nagy Ábel, Németh 729 Gábor, Olexó Gergely, Radnai Bálint, Rittgasszer Ákos, Uzonyi 000 Ákos. 9 points: Jakab 042 Richárd, Szakali Benedek, Tersztenyák Balázs. 8 points: 1 student.
Problems in Information Technology of KöMaL, September 2015
