K. 117. A sheet of paper is folded in three along the dotted lines as shown in the Figure. (Each crease may have an arbitrary direction.) The creases divide the two sides of the sheet into six parts altogether. Each of the six parts is coloured in a different colour, and the sheet is folded again along the original lines. Then there will be only two parts that can be seen. How many different pairs of colours may result from different ways of folding the sheet?

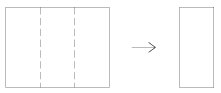
(6 points)

Deadline expired.

Sorry, the solution is published in Hungarian only.

Megoldás. Minden résznek két másik lehet a párja (1-esnek 2-es és 6-os; 2-esnek 1-es és 3-as; 3-asnak 2-es és 4-es, 4-esnek 5-ös és 3-as, 5-ösnek 4-es és 6-os, 6-osnak 1-es és 5-ös), ez összesen 12 lehetséges pár, de mindegyiket mindkettőnél megszámoltuk, így ennek fele, azaz 6 lehetséges színpárosítás van.

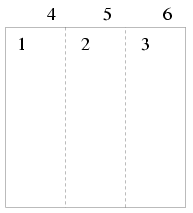
Statistics on problem K. 117. 137 students sent a solution. 6 points: 100 students. 5 points: 23 students. 4 points: 4 students. 2 points: 5 students. 1 point: 1 student. 0 point: 3 students. Unfair, not evaluated: 1 solution.