 Problem K. 123. (March 2007)
Problem K. 123. (March 2007)
K. 123. Three bunnies are sitting in the grass. There is a heap of carrots in front of each of them, 36 carrots altogether. Suppose they simultaneously pass some carrots to one another: the first bunny passes one third of his carrots to the second one, the second one passes one fourth of his carrots to the third one, and the third bunny passes one fifth of his carrots to the first one. As a result, each bunny will have the same amount of carrots as initially. How many carrots does each of them have?
(6 pont)
Deadline expired on April 10, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Ahhoz, hogy mindenkinek annyi répája legyen a végén, mint az elején, az kell, hogy mindenki ugyanannyit adjon, mint amennyit kap, azaz
1/3 E=1/4 M=1/5 H 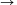 3/5 H+4/5 H+H=36,
3/5 H+4/5 H+H=36,
ahonnan H=15, M=12, E=9.
Statistics:
120 students sent a solution. 6 points: 63 students. 5 points: 21 students. 4 points: 14 students. 3 points: 3 students. 2 points: 7 students. Unfair, not evaluated: 12 solutionss.
Problems in Mathematics of KöMaL, March 2007
