 Problem K. 131. (September 2007)
Problem K. 131. (September 2007)
K. 131. There is a rectangular food box on the kitchen counter. Its outer dimensions are 3 dm×5 dm×2.9 dm. The box is standing on its 3×5-dm face. An ant is crawling from one lower corner to the diagonally opposite top corner on the outer surface of the box. (It cannot get in the interior of the box.) What is the shortest distance that it needs to cover?
(6 pont)
Deadline expired on October 10, 2007.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Hajtogassuk szét a doboz oldalait! A doboz teteje az a téglalap, melyen az A pont van jelölve, ez a célpont, melyet B-ből indulva kell elérnie a hangyának. A legrövidebb út úgy adódhat, hogy a B pontból valamelyik oldallapon indul az A pont felé, és felmegy a doboz tetejére. Ezt a három utat az ábrákon szaggatott vonallal jelöltük.
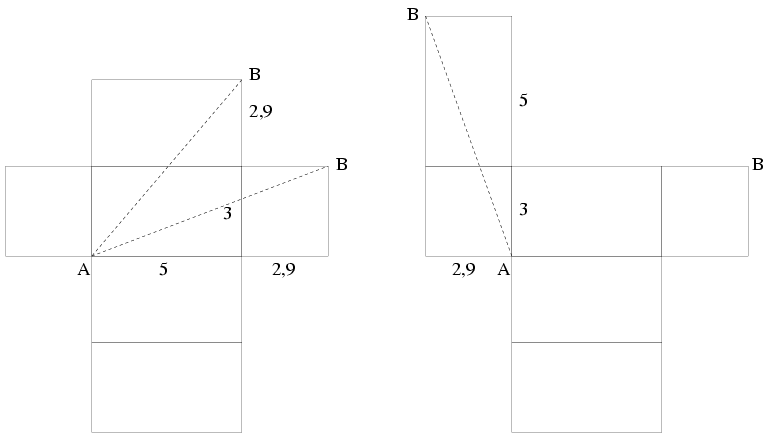
A Pitagorasz-tétel segítségével számítható ezek hossza: ,
,
. Tehát a bal ábrán jelölt felső út a legrövidebb, hossza kb. 7,73 dm.
Statistics:
301 students sent a solution. 6 points: Ábrahám Máté, Árvay Balázs, Babits Réka, Bartha Kristóf, Bicskei Dávid, Boross Gergely, Borza Ágnes, Doma Péter, Farkas Zsuzsanna, Klausz Milán, Pánczél János Károly, Pós Eszter Sarolta, Sass Zoltán, Slenker Dániel, Tátrai Kinga, Tene Zsuzsanna, Ván Bálint, Varga 107 Nátán, Várnai Péter, Zempléni Réka. 5 points: Bálint Máté, Czebe 007 Brigitta, Köpenczei Gergő, Kunos Vid, Roboz Klaudia, Viczán Gergely. 4 points: 45 students. 3 points: 112 students. 2 points: 5 students. 1 point: 6 students. 0 point: 104 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, September 2007
