Problem K. 142. (November 2007)

K. 142. In the Mathematical Olympiad of 2100, gold and silver medals will be made of pure gold and silver (and bronze medals will be made of bronze). The diameter of the silver medal will be 3 cm, with a thickness of 5 mm. (The shape of the medals will be as usual.) What will be the diameters of the gold and bronze medals if all the three kinds of medal have the same mass and thickness? (Densities: gold $19\;300~\rm kg/m^{3}$ , silver $10\;500~\rm kg/m^{3}$ , bronze 8930 kg/m³.)

(6 pont)

Deadline expired on December 10, 2007.

Sorry, the solution is available only in Hungarian. Google translation

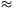Megoldás: Az ezüstérem tömege m_e=0,015²^. $\pi$ ^.0,005^.10500 $\approx$ 0,037 kg. Ugyanilyen tömegű aranyérem térfogata 0,037 kg=r_a²^. $\pi$ ^.0,005^.19300, amiből az aranyérem sugara kb. 0,011 m. Hasonlóan a bronzéremre 0,037 kg=r_b²^. $\pi$ ^.0,005^.8930, ahonnan a bronzérem sugara kb. 0,016 m.

Statistics:

207 students sent a solution.

6 points: 115 students.

5 points: 35 students.

4 points: 18 students.

3 points: 14 students.

2 points: 8 students.

1 point: 7 students.

0 point: 4 students.

Unfair, not evaluated: 6 solutionss.

Problems in Mathematics of KöMaL, November 2007

207 students sent a solution.
6 points:	115 students.
5 points:	35 students.
4 points:	18 students.
3 points:	14 students.
2 points:	8 students.
1 point:	7 students.
0 point:	4 students.
Unfair, not evaluated:	6 solutionss.

Already signed up?
New to KöMaL?