 Problem K. 155. (January 2008)
Problem K. 155. (January 2008)
K. 155. In the triangle shown in the Figure,  DAB=
DAB= ABC=60o, and
ABC=60o, and  CAB=
CAB= CBD. Prove that AD+CB=AB.
CBD. Prove that AD+CB=AB.
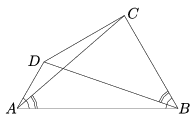
(6 pont)
Deadline expired on February 11, 2008.
Sorry, the solution is available only in Hungarian. Google translation
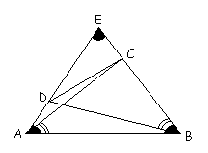
Megoldás. Az AD és CB oldalakat meghosszabbítva egy szabályos háromszöget kapunk. Az ABC háromszög és az EDB háromszög egybevágó, hiszen AB=EB és a három szögük is megegyezik. A két háromszög egybevágóságából következik, hogy megfelelő oldalai egyenlők, azaz CB=DE, így AD+CB=AD+DE=AE=AB.
Statistics:
128 students sent a solution. 6 points: 70 students. 5 points: 22 students. 4 points: 10 students. 3 points: 3 students. 2 points: 7 students. 1 point: 9 students. 0 point: 6 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, January 2008
