Problem K. 156. (January 2008)

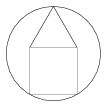
K. 156. The lower part of the house (see the Figure) in the circle is a square, and the top is an equilateral triangle. Prove that the length of the side of the house equals the radius of the circle.

(6 pont)

Deadline expired on February 11, 2008.

Sorry, the solution is available only in Hungarian. Google translation

Megoldás. Kössük össze a kör középpontjával a ház E csúcsát, és B sarkát.

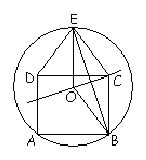
CB=CD=EC, tehát az ECB háromszög egyenlő szárú, alapon fekvő szögei egyenlőek, nagyságuk pedig: $BEC\angle=EBC\angle=\frac{180^{\circ}-ECB\angle}{2}=\frac{180^{\circ}-(60^{\circ}+90^{\circ})}{2}=15^{\circ}$ .

EO=OB=r, így az $EOB_{\triangle}$ egyenlő szárú, és így alapon fekvő szögei egyenlőek: $OBE\angle=OEB\angle=OEC\angle-BEC\angle=\frac{60^{\circ}}{2}-BEC\angle=30^{\circ}-15^{\circ}=15^{\circ}$ . (Felhasználtuk, hogy EO felezi a DEC $\angle$ -et.)

$EOB_{\triangle}$ egybevágó az $ECB_{\triangle}$ -gel, hiszen alapjuk és az azon fekvő szögek egyenlőek. Ennélfogva száraik is egyenlő hosszúak, vagyis a kör sugara megegyezik a ház oldalával.

Statistics:

125 students sent a solution.

6 points: 60 students.

5 points: 13 students.

4 points: 7 students.

3 points: 5 students.

2 points: 9 students.

1 point: 14 students.

0 point: 16 students.

Unfair, not evaluated: 1 solutions.

Problems in Mathematics of KöMaL, January 2008

125 students sent a solution.
6 points:	60 students.
5 points:	13 students.
4 points:	7 students.
3 points:	5 students.
2 points:	9 students.
1 point:	14 students.
0 point:	16 students.
Unfair, not evaluated:	1 solutions.

Already signed up?
New to KöMaL?