 Problem K. 158. (February 2008)
Problem K. 158. (February 2008)
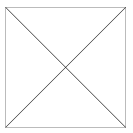
K. 158. A square garden is formed in a park out of four flowerbeds (as shown in the Figure). A single type of flowers are planted in each flowerbed, so that adjacent beds contain different types. (It is allowed to plant the same type of flower in opposite beds.) The flowers are selected out of three types: roses, lilies or gladioluses. In how many different ways can the garden be organized if orientation matters, too (that is, if it makes a difference which kind of flowers are planted in the north, south, east and west flowerbed)?
(6 pont)
Deadline expired on March 10, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás. Mivel csak háromféle virágunk van, ezért két virágágyásba azonos fajtájú virágok fognak kerülni. A feltételek miatt ezek csak szemközti ágyások lehetnek. Ennek megfelelően a virágokat három típusú elrendezésben helyezhetjük el az ágyásokban annak megfelelően, hogy mely ágyásokba kerülnek azonos fajtájú virágok:
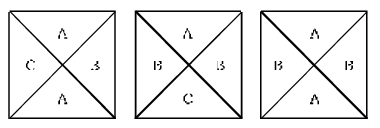
Minden esetben az A-val jelölt helyre 3-féle, a B-vel jelölt helyre 2-féle, a C-vel jelölt helyre 1-féle fajtájú virág kerülhet. Így minden esetben a lehetőségek száma 3.2=6, összesen 18. Tehát összesen 18-féleképpen alakítható ki a virágoskert.
Statistics:
137 students sent a solution. 6 points: 95 students. 5 points: 1 student. 4 points: 5 students. 3 points: 13 students. 2 points: 4 students. 1 point: 1 student. 0 point: 15 students. Unfair, not evaluated: 3 solutionss.
Problems in Mathematics of KöMaL, February 2008
