Problem K. 165. (March 2008)

K. 165. Billy and Sophie are making rings out of paper strips and link them together to form chains. Each of them uses a 21×30 cm sheet of paper for making the chain. Billy cuts up the sheet parallel to the 21-cm sides, and a Sophie cuts it parallel to the 30-cm sides. Both of them make strips 1 cm wide, curve them into rings and glue them with 0-cm overlaps. The rings link together to form a chain without any deformation. Which chain is longer? (In calculating the perimeter of a circle, use 3.14 for the value of $\pi$ , and disregard the thickness of the paper.)

(6 pont)

Deadline expired on April 10, 2008.

Sorry, the solution is available only in Hungarian. Google translation

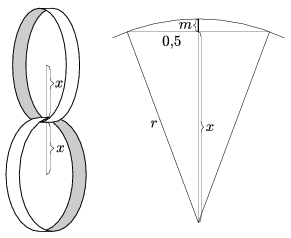
I. megoldás: Balázs 21 cm hosszú papírcsíkokat vág, és ebből van neki 30 db. Mivel a ragasztásnál nincs átfedés, egy karikájának sugara $r=\frac{21}{2\pi} \approx 3,34$ cm. Mint az ábrán látszik, a karikák a találkozásuknál megemelik egy kicsit egymást annyival, amekkora egy 1 cm-es húr által levágott körszelet m magassága. Az ábrán x=r-m jelöli azt a hosszt, amivel számolnunk kell a lánc hosszának megállapításakor. A Pitagorasz-tétel alkalmazásával: $x=\sqrt{r^2-0{,}5^2} \approx 3{,}30$ cm. A 30 db karika 30^.2^.3,30+31^.(3,34-3,30)=199,24 cm hosszú láncot alkot.

Zsófi 30 cm hosszú papírcsíkokat vág, és ebből van neki 21 db. Egy karikájának sugara $\frac{30}{2\pi} \approx 4{,}78$ cm, amiből x=4,75 cm, a 21 db karika tehát 21^.2^.4,75+22^.(4,78-4,75)=200,16 cm hosszú láncot alkot. Tehát Zsófi lánca hosszabb, mint Balázsé.

II. megoldás: Balázs karikájának kerülete kevesebb (21 cm), mint Zsófi karikájának kerülete (30 cm). Egy kisebb kerületű körlemezből ugyanolyan hosszú húr (1 cm) nagyobb magasságú körszeletet vág le, mint egy nagyobb kerületűből. Tehát egy 21 cm kerületű karikákból készülő lánc többet veszít a hosszából, mint egy ugyanannyi darab 30 cm kerületű karikából álló lánc. Balázsnak ráadásul több karikája is van (30 darab), mint Zsófinak (21 darab), tehát a lánca még többet veszít a hosszából. Ezek alapján Zsófi lánca hosszabb lesz, mint Balázsé.

Statistics:

144 students sent a solution.

6 points: Csernyánszky Nándor, Hegedűs Csaba, Pánczél János Károly, Pere Tamás, Tene Zsuzsanna, Varga 777 Ádám.

5 points: Blóz Gizella Evelin, Kunos Vid, Rudas Csilla, Várnai Péter.

4 points: 1 student.

3 points: 4 students.

2 points: 122 students.

1 point: 3 students.

0 point: 2 students.

Unfair, not evaluated: 2 solutionss.

Problems in Mathematics of KöMaL, March 2008

144 students sent a solution.
6 points:	Csernyánszky Nándor, Hegedűs Csaba, Pánczél János Károly, Pere Tamás, Tene Zsuzsanna, Varga 777 Ádám.
5 points:	Blóz Gizella Evelin, Kunos Vid, Rudas Csilla, Várnai Péter.
4 points:	1 student.
3 points:	4 students.
2 points:	122 students.
1 point:	3 students.
0 point:	2 students.
Unfair, not evaluated:	2 solutionss.

Already signed up?
New to KöMaL?