 Problem K. 166. (March 2008)
Problem K. 166. (March 2008)
K. 166. Alex is building a pyramid out of congruent cubes, following to the pattern. (He uses no glue, only places the cubes simply next to on top of each other.) Each vertical layer is two cubes taller than the previous one, and forms ascending steps on both sides. When Alex has reached the height of 10 cubes, he goes on decreasing the height of the layers by two cubes in the same fashion. How many cubes does he use altogether?
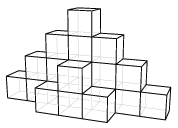
(6 pont)
Deadline expired on April 10, 2008.
Sorry, the solution is available only in Hungarian. Google translation
Megoldás: Észrevehető, hogy minden függőleges réteg átdarabolható egy négyzetes elrendezésbe:
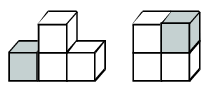
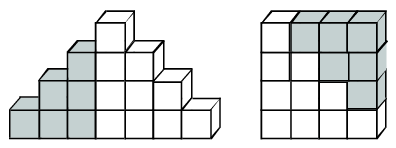
Mivel a rétegek magassága mindig kettővel nő, ezért a páros négyzetszámok adják meg a szomszédos rétegekben levő kockák darabszámát. Tehát a keresett darabszám: 4+16+36+64+100+64+36+16+4=340.
Statistics:
136 students sent a solution. 6 points: 74 students. 5 points: 13 students. 4 points: 24 students. 3 points: 11 students. 2 points: 2 students. 1 point: 2 students. 0 point: 9 students. Unfair, not evaluated: 1 solutions.
Problems in Mathematics of KöMaL, March 2008
