 |
A K. 210. feladat (2009. március) |
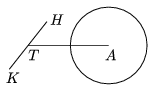
K. 210. Az ábrán Dóri kisbiciklijének részlete látható. A hátsó kerék középpontja A, a TK hajtókar (melynek végén található az egyik pedál) pedig a T pont körül forog. Tekintsük az A, K, T pontokat egysíkúnak. A TK hossza 20 cm, AT hossza 48 cm. Hány olyan helyzete van a K pontnak, miközben a hajtókar T körül körbefordul, amikor az AK távolság cm-ben mérve egész szám, és az AKT háromszög hegyesszögű?
(6 pont)
A beküldési határidő 2009. április 10-én LEJÁRT.
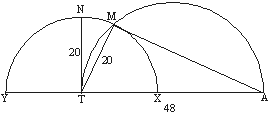
Megoldás. A szimmetria miatt elég megnézni, hogy hány kívánt helyzet van a TA egyenes feletti részben. A K végpont az X ponttól az Y pontig halad a T középpontú, 20 cm sugarú köríven. Mindaddig, amíg TA szakasz Thalész-körén belül van, a TKA szög tompaszög, így ott nincs megfelelő helyzet. Amint kilépünk TA szakasz Thalész-körén kívülre, a TKA szög hegyesszöggé válik. Amint elérjük az N pontot, a továbbiakban ismét nem találtunk hegyesszögű háromszöget, mert az ATK szög válik tompaszöggé. Amíg K az N és M között van, az ATK háromszög hegyesszögű, mert a TAK szög K minden helyzetében nyilvánvalóan hegyesszög. Az MA távolság Pitagorasz-tételéből számítható: cm, az NA távolság szintén a Pitagorasz-tételből
cm. Könnyen látható, hogy miközben a K pont X-ből Y-ba megy, az AK távolság folyamatosan nő (ha egy háromszög két oldala rögzített és a közbezárt szögük folyamatosan nő, akkor a harmadik oldal is folyamatosan nő), tehát az AK távolság lehetséges értékei 44, 45, ..., 51, ez összesen 8 db helyzetet jelent. A TA másik oldalán is 8 db megfelelő helyzetet találunk, tehát összesen 16 db olyan helyzete van a K pontnak, melyben a feltételek teljesülnek.
Statisztika:
87 dolgozat érkezett. 6 pontot kapott: Bende Lilla, Budafoki Dóra, Gujás István, Halász 423 Dániel, Karádi 468 Dániel Tamás, Kasó Márton, Kis Attila Soma, Könye Viktor, Kővágó Zoltán, Nagy Zsuzsanna, Nánási József, Pizág Bertalan, Rónaky Rebeka, Samu Viktor, Sándor Tímea, Sápi András, Straubinger Dániel, Szigeti Bertalan György, Táczi István, Tolnai Dániel, Zagyva Dániel. 5 pontot kapott: Bagó Bence, Bauer Barbara, Borbély Roland, Böröndy Áron, Bulla Ádám, Fazekas Gábor László, Félegyházi Dávid, Halász Dániel, Hoszták Ákos, Juhász-Bóka Bernadett, Kovács Péter, Merczel Kinga, Mezey Márton, Miklós-Kovács Janka, Serfőző Virág Fanni, Solti Bálint, Szabó Gréta, Tarcza Anna, Tornóczky Márton, Vámi Tamás Álmos, Veres Andrea, Wiszt Attila. 4 pontot kapott: 13 versenyző. 3 pontot kapott: 4 versenyző. 2 pontot kapott: 2 versenyző. 1 pontot kapott: 12 versenyző. 0 pontot kapott: 11 versenyző. Nem versenyszerű: 2 dolgozat.
A KöMaL 2009. márciusi matematika feladatai

